
在图①至图③中,已知△ABC的面积为 .
.
(1)如图①,延长△ABC的边BC到点D,使CD=BC,连结DA。若△ACD的面积为S1,则S1=______(用含 的代数式表示);
的代数式表示);
(2)如图②,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2=__________(用含 的代数式表示);
的代数式表示);
(3)在图①—②的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图③).
阴影部分的面积为S3,则S3=__________(用含 的代数式表示),并运用上述(2)的结论写出理由.
的代数式表示),并运用上述(2)的结论写出理由.
理由:

(1)a;(2)2a;(3)6a; 等底同高的三角形面积相等.
【解析】
试题分析:(1)由三角形ABC与三角形ACD中BC=CD,且这两边上的高为同一条高,根据等底同高即可得到两三角形面积相等,由三角形ABC的面积即可得到三角形ACD的面积,即为S1的值.
(2)连接AD,由CD=BC,且三角形ABC与三角形ACD同高,根据等底同高得到两三角形面积相等,同理可得三角形ABC与三角形ADC面积相等,而三角形CDE面积等于两三角形面积之和,进而表示出三角形CDE的面积.
(3)根据第二问的思路,同理可得阴影部分的面积等于3S2,由S2即可表示出S3.
试题解析:(1)∵BC=CD,且△ABC与△ACD同高,
∴S△ABC=S△ADC,又S△ABC=a. ∴S△ADC=a.
(2)连接AD,如图2所示,
∵BC=CD,且△ABC与△ACD同高,∴S△ABC=S△ADC=a.
同理S△ADE=S△ADC=a,∴S△CDE=2S△ABC=2a.
(3)如图3,连接AD,EB,FC,
同理可得:S△AEF=S△BFD=S△CDE,
则阴影部分的面积为S3=3S△CDE=6a.
理由: 等底同高的三角形面积相等.

考点:等腰三角形的性质;三角形的面积.


科目:初中数学 来源:2015届北京市房山区八年级下学期期末考试数学试卷(解析版) 题型:解答题
如图,正方形ABCD的两条对角线把正方形分割成四个等腰直角三角形,将这四个三角形分别沿正方形ABCD的边向外翻折,可得到一个新正方形EFGH.请你在矩形ABCD中画出分割线,将矩形分割成四个三角形,然后分别将这四个三角形沿矩形的边向外翻折,使得图1得到菱形,图2得到矩形,图3得到一般的平行四边形(只在矩形ABCD中画出分割线,说明分割线的作法,不画出翻折后的图形).

查看答案和解析>>
科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:选择题
下列命题中,真命题是( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是直角梯形
C.四个角相等的菱形是正方形
D.两条对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源:2015届云南省八年级上学期期末考试数学试卷(解析版) 题型:解答题
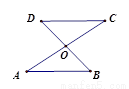
如图,AC交BD于点O,请你从三项中选出两个作为条件,另一个作为结论,写出一个真命题,并加以证明.
①OA=OC ②OB=OD ③AB∥CD
查看答案和解析>>
科目:初中数学 来源:2014年江西省吉安市吉州区九年级下学期第一次中考模拟数学试卷(解析版) 题型:解答题
为响应吉安市2014年创建国家级卫生城市的号召,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图。
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率。

查看答案和解析>>
科目:初中数学 来源:2014年北京市西城区中考二模数学试卷(解析版) 题型:选择题
如图,四边形ABCD为⊙O的内接四边形,若∠BCD=110°,则∠BAD的度数为( )
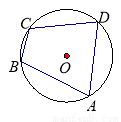
A.140° B.110° C.90° D.70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com