
ЎҫМвДҝЎҝИзНјФЪіӨ·ҪРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬өг
Ј¬өг![]() ҙУ
ҙУ![]() өгіц·ўЈ¬СШ
өгіц·ўЈ¬СШ![]() В·ПЯФЛ¶ҜЈ¬өҪ
В·ПЯФЛ¶ҜЈ¬өҪ![]() өгНЈЦ№;өг
өгНЈЦ№;өг![]() ҙУ
ҙУ![]() өгіц·ўЈ¬СШ
өгіц·ўЈ¬СШ![]() ФЛ¶ҜЈ¬өҪ
ФЛ¶ҜЈ¬өҪ![]() өгНЈЦ№Ифөг
өгНЈЦ№Ифөг![]() Ўўөг
Ўўөг![]() Н¬Кұіц·ўЈ¬өг
Н¬Кұіц·ўЈ¬өг![]() өДЛЩ¶ИОӘГҝГл
өДЛЩ¶ИОӘГҝГл![]() Ј¬өг
Ј¬өг![]() өДЛЩ¶ИОӘГҝГл
өДЛЩ¶ИОӘГҝГл![]() Ј¬УГ
Ј¬УГ![]() ЈЁГлЈ©ұнКҫФЛ¶ҜКұјдЈ®
ЈЁГлЈ©ұнКҫФЛ¶ҜКұјдЈ®
ЈЁ1Ј©өұ![]() __________ГлКұЈ¬өг
__________ГлКұЈ¬өг![]() әНөг
әНөг![]() ПаУцЈ®
ПаУцЈ®
ЈЁ2Ј©Б¬ҪУ![]() Ј¬өұ
Ј¬өұ![]() ЖҪ·ЦіӨ·ҪРО
ЖҪ·ЦіӨ·ҪРО![]() өДГж»эКұЈ¬ЗуҙЛКұ
өДГж»эКұЈ¬ЗуҙЛКұ![]() өДЦө
өДЦө
ЈЁ3Ј©Ифөг![]() Ўўөг
Ўўөг![]() ФЛ¶ҜөҪ6ГлКұН¬КұёДұдЛЩ¶ИЈ¬өг
ФЛ¶ҜөҪ6ГлКұН¬КұёДұдЛЩ¶ИЈ¬өг![]() өДЛЩ¶ИұдОӘГҝГл
өДЛЩ¶ИұдОӘГҝГл![]() Ј¬өг
Ј¬өг![]() өДЛЩ¶ИұдОӘГҝГл
өДЛЩ¶ИұдОӘГҝГл![]() Ј¬ЗуФЪХыёцФЛ¶Ҝ№эіМЦРЈ¬өг
Ј¬ЗуФЪХыёцФЛ¶Ҝ№эіМЦРЈ¬өг![]() өг
өг![]() ФЪФЛ¶ҜВ·ПЯЙППаҫаВ·іМОӘ
ФЪФЛ¶ҜВ·ПЯЙППаҫаВ·іМОӘ![]() КұФЛ¶ҜКұјд
КұФЛ¶ҜКұјд![]() өДЦөЈ®
өДЦөЈ®



Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©4»т20Ј»ЈЁ3Ј©4»т14.5
Ј»ЈЁ2Ј©4»т20Ј»ЈЁ3Ј©4»т14.5
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭөгPФЛ¶ҜөДВ·іМ+өгQФЛ¶ҜөДВ·іМ=И«іМіӨ¶ИЈ¬јҙҝЙөГіц№ШУЪxөДТ»ФӘТ»ҙО·ҪіМЈ¬ҪвЦ®јҙҝЙөГіцҪбВЫЈ»
ЈЁ2Ј©·ЦөгPФЪABұЯЙПКұЈ¬өгQФЪCDұЯЙПәНөгQФЛ¶ҜөҪAөгЈ¬өгPФЛ¶ҜөҪөгCБҪЦЦЗйҝцҪшРРМЦВЫјҙҝЙЗуҪвЈ®
ЈЁ3Ј©ПИ·ЦОцұдЛЩЗ°әНұдЛЩәуБҪЦЦЗйҝцҪшРРјҙҝЙөГЈ®
ЈЁ1Ј©ёщҫЭМвТвөГЈәx+2x=12ЎБ2+8Ј¬
ҪвөГЈәx=![]() Ј®
Ј®
№Кҙр°ёЈәөұxөДЦөОӘ![]() КұЈ¬өгPәНөгQПаУцЈ®
КұЈ¬өгPәНөгQПаУцЈ®
ЈЁ2Ј©ЎЯPQЖҪ·ЦҫШРОABCDөДГж»эЈ¬
өұөгPФЪABұЯЙПКұЈ¬өгQФЪCDұЯЙПЈ¬
УРМвТвҝЙЦӘЈә2x=12xЈ¬
ҪвөГЈәx=4Ј®
өұөгQФЛ¶ҜөҪөгAКұЈ¬УГКұ(12+8+12)ЎВ2=16ГлЈ¬ҙЛКұөгPФЛ¶ҜөҪөгCКұЈ¬PQЖҪ·ЦҫШРОABCDГж»эЈ¬ҙЛКұУГКұЈә(12+8)ЎВ1=20Гл
№Кҙр°ёЈәөұФЛ¶Ҝ4Гл»т20ГлКұЈ¬PQЖҪ·ЦҫШРОABCDөДГж»эЈ®
ЈЁ3Ј©ұдЛЩЗ°Јәx+2x=32-20
ҪвөГx=4
ұдЛЩәуЈә12+(x-6)+6+3ЎБ(x-6)=32+20
ҪвөГx=14.5
ЧЫЙПЛщКцЈәxөДЦөОӘ4»т14.5


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
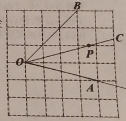
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬AЈ¬BЈ¬CИэөгөДЧшұк·ЦұрОӘЈЁ©Ғ6Ј¬7Ј©Ј¬ЈЁ©Ғ3Ј¬0Ј©Ј¬ЈЁ0Ј¬3Ј©Ј®
ЈЁ1Ј©»ӯіцИэҪЗРОABCЈ¬ІўЗуИэҪЗРОABCөДГж»эЈ»
ЈЁ2Ј©Ҫ«ИэҪЗРОABCЖҪТЖөГөҪИэҪЗРОAЎдBЎдCЎдЈ¬өгCҫӯ№эЖҪТЖәуөД¶ФУҰөгОӘCЎдЈЁ5Ј¬4Ј©Ј¬»ӯіцЖҪТЖәуөДИэҪЗРОAЎдBЎдCЎдЈ¬ІўРҙіцөгAЎдЈ¬BЎдөДЧшұкЈәAЎдЈЁ________Ј©Ј¬BЎдЈЁ________Ј©
ЈЁ3Ј©ТСЦӘөгPЈЁ©Ғ3Ј¬mЈ©ОӘИэҪЗРОABCДЪТ»өгЈ¬Ҫ«өгPПтУТЖҪТЖ4ёцөҘО»әуЈ¬ФЩПтПВЖҪТЖ6ёцөҘО»өГөҪөгQЈЁnЈ¬©Ғ3Ј©Ј¬ФтmЈҪ________Ј¬nЈҪ________Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
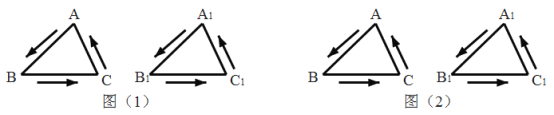
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬AB ЈҪACЈ¬ADЎНBCУЪөгDЈ¬AMКЗЎчABCөДНвҪЗЎПCAEөДЖҪ·ЦПЯЈ®
(1)ЗуЦӨЈәAMЎОBCЈ»
(2)ИфDNЖҪ·ЦЎПADCҪ»AMУЪөгNЈ¬ЕР¶ПЎчADNөДРОЧҙІўЛөГчАнУЙЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ГҝёцНј°ёҫщУЙұЯіӨПаөИөДәЪЎў°ЧБҪЙ«Хэ·ҪРО°ҙ№жВЙЖҙҪУ¶шіЙЈ¬ХХҙЛ№жВЙЈ¬өЪnёцНј°ёЦР°ЧЙ«Хэ·ҪРОұИәЪЙ«Хэ·ҪРО¶а________ёц.ЈЁУГә¬nөДҙъКэКҪұнКҫЈ©

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬өг![]() КЗ
КЗ![]() өДҪЗЖҪ·ЦПЯ
өДҪЗЖҪ·ЦПЯ![]() ЙПИОТвТ»өгЈ¬
ЙПИОТвТ»өгЈ¬
ЈЁ1Ј©№эөг![]() ·Цұр»ӯ
·Цұр»ӯ![]() Ўў
Ўў![]() өДҙ№ПЯЈ¬ҙ№Чг·ЦұрОӘ
өДҙ№ПЯЈ¬ҙ№Чг·ЦұрОӘ![]() Ј¬
Ј¬![]() Ј®ІўНЁ№эІвБҝ·ўПЦ
Ј®ІўНЁ№эІвБҝ·ўПЦ![]() __________
__________![]() ЈЁМоЎ°
ЈЁМоЎ°![]() Ўұ»тЎ°
Ўұ»тЎ°![]() Ўұ»тЎ°
Ўұ»тЎ°![]() ЎұЈ©
ЎұЈ©
ЈЁ2Ј©№эөг![]() »ӯ
»ӯ![]() өДЖҪРРПЯЈ¬Ҫ»
өДЖҪРРПЯЈ¬Ҫ»![]() УЪөг
УЪөг![]() Ј®НЁ№эІвБҝ·ўПЦ
Ј®НЁ№эІвБҝ·ўПЦ![]() __________
__________![]() ЈЁМоЎ°
ЈЁМоЎ°![]() Ўұ»тЎ°
Ўұ»тЎ°![]() Ўұ»тЎ°
Ўұ»тЎ°![]() ЎұЈ©
ЎұЈ©
ЈЁ3Ј©ЦұҪУЕР¶П![]() Ул
Ул![]() өДҙуРЎ№ШПөЈ¬ІўЛөГчАнУЙЈ®
өДҙуРЎ№ШПөЈ¬ІўЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘөчІйКРГсЙП°аКұЧоіЈУГөДҪ»НЁ№ӨҫЯөДЗйҝцЈ¬Лж»ъійИЎБЛЛДКРІҝ·ЦКРГсҪшРРөчІй,ТӘЗуұ»өчІйХЯҙУЎ°AЈәЧФРРіөЈ¬BЈәөз¶ҜіөЈ¬CЈә№«Ҫ»іөЈ¬DЈәјТНҘЖыіөЈ¬EЈәЖдЛыЎұОеёцСЎПоЦРСЎФсЧоіЈУГөДТ»ПоЈ¬Ҫ«ЛщУРөчІйҪб№ыХыАнәу»жЦЖіЙИзПВІ»НкХыөДМхРОНіјЖНјәНЙИРОНіјЖНјЈ¬ЗлҪбәПНіјЖНј»ШҙрПВБРОКМвЈә
ЈЁ1Ј©ФЪХвҙОөчІйЦРЈ¬Т»№ІөчІйБЛ ГыКРГсЈ®
ЈЁ2Ј©ЙИРОНіјЖНјЦРЈ¬CЧй¶ФУҰөДЙИРОФІРДҪЗКЗ Ј®
ЈЁ3Ј©ЗлІ№И«МхРОНіјЖНјЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈәФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ИэҪЗРОABCөД¶ҘөгЧшұк·ЦұрКЗA(1Ј¬1)Ј»B(2Ј¬©Ғ1)Ј»C(4Ј¬3)Ј¬Ҫ«ИэҪЗРОABCПтЧуЖҪТЖ2ёцөҘО»іӨ¶ИЈ¬ФЩПтЙПЖҪТЖ3ёцөҘО»іӨ¶ИәуөГИэҪЗРОA1B1C1Ј®
ЈЁ1Ј©»ӯіцИэҪЗРОA1B1C1Ј»
ЈЁ2Ј©·ЦұрРҙіцA1ЎўB1ЎўC1өДЧшұкЈ»
ЈЁ3Ј©ЗуИэҪЗРОA1B1C1өДГж»эЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИ«өИИэҪЗРОУЦҪРЧцәПН¬ИэҪЗРОЈ¬ЖҪГжДЪөДәПН¬ИэҪЗРО·ЦОӘХжХэәПН¬ИэҪЗРОУлҫөГжәПН¬ИэҪЗРОЈ¬јЩЙиЎчABCәНЎчA1B1C1КЗәПН¬ИэҪЗРОЈ¬өгAУлөгA1¶ФУҰЈ¬өгBУлөгB1¶ФУҰЈ¬өгCУлөгC1¶ФУҰЈ¬өұСШЦЬҪзAЎъBЎъCЎъAЈ¬ј°A1ЎъB1ЎъC1ЎъA1»·ИЖКұЈ¬ИфФЛ¶Ҝ·ҪПтПаН¬Ј¬ФтіЖЛьГЗКЗХжХэәПН¬ИэҪЗРОЈЁИзНј1Ј©Ј¬ИфФЛ¶Ҝ·ҪПтПа·ҙЈ¬ФтіЖЛьГЗКЗҫөГжәПН¬ИэҪЗРОЈЁИзНј2Ј©Ј¬БҪёцХжХэәПН¬ИэҪЗРО¶јҝЙТФФЪЖҪГжДЪНЁ№эЖҪТЖ»тРэЧӘК№ЛьГЗЦШәПЈ¬БҪёцҫөГжәПН¬ИэҪЗРОТӘЦШәПЈ¬ФтұШРлҪ«ЖдЦРТ»ёц·ӯЧӘ180Ўг.ПВБРёчЧйәПН¬ИэҪЗРОЦРЈ¬КЗҫөГжәПН¬ИэҪЗРОөДКЗЈЁ Ј©
A. B.
B. C.
C.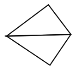 D.
D.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈјЖ»®ҙУёч°аёчійіц1ГыС§ЙъЧчОӘҙъұнІОјУѧУЧйЦҜөДәЈНвУОС§јЖ»®Ј¬ГчГчәН»Ә»Ә¶јКЗұҫ°аөДәтСЎИЛЈ¬ҫӯ№эАПКҰУлН¬С§ГЗЙМБҝЈ¬УГЛщС§өДёЕВКЦӘК¶ЙијЖГюЗтУОП·ҫц¶ЁЛӯИҘЈ¬ЙијЖөДУОП·№жФтИзПВЈәИЎMЎўNБҪёцІ»НёГчөДІјҙьЈ¬·Цұр·ЕИл»ЖЙ«әН°ЧЙ«БҪЦЦіэСХЙ«НвҫщПаН¬өДЖ№ЕТЗтЈ¬ЖдЦРMІјҙьЦР·ЕЦГ3ёц»ЖЙ«өДЖ№ЕТЗтәН2ёц°ЧЙ«өДЖ№ЕТЗтЈ»NІјҙьЦР·ЕЦГ1ёц»ЖЙ«өДЖ№ЕТЗтЈ¬3ёц°ЧЙ«өДЖ№ЕТЗт![]() ГчГчҙУMІјҙьГюТ»ёцЖ№ЕТЗтЈ¬»Ә»ӘҙУNІјҙьГюТ»ёцЖ№ЕТЗтҪшРРКФСйЈ¬ИфБҪИЛГюіцөДБҪёцЖ№ЕТЗт¶јКЗ»ЖЙ«Ј¬ФтГчГчИҘЈ»ИфБҪИЛГюіцөДБҪёцЖ№ЕТЗт¶јКЗ°ЧЙ«Ј¬Фт»Ә»ӘИҘЈ»ИфБҪИЛГюіцЖ№ЕТЗтСХЙ«І»Т»СщЈ¬Фт·Е»ШЦШёҙТФЙП¶ҜЧчЈ¬ЦұөҪ·ЦіцКӨёәОӘЦ№
ГчГчҙУMІјҙьГюТ»ёцЖ№ЕТЗтЈ¬»Ә»ӘҙУNІјҙьГюТ»ёцЖ№ЕТЗтҪшРРКФСйЈ¬ИфБҪИЛГюіцөДБҪёцЖ№ЕТЗт¶јКЗ»ЖЙ«Ј¬ФтГчГчИҘЈ»ИфБҪИЛГюіцөДБҪёцЖ№ЕТЗт¶јКЗ°ЧЙ«Ј¬Фт»Ә»ӘИҘЈ»ИфБҪИЛГюіцЖ№ЕТЗтСХЙ«І»Т»СщЈ¬Фт·Е»ШЦШёҙТФЙП¶ҜЧчЈ¬ЦұөҪ·ЦіцКӨёәОӘЦ№![]() ёщҫЭТФЙП№жФт»ШҙрПВБРЈә
ёщҫЭТФЙП№жФт»ШҙрПВБРЈә
![]() ЗуТ»ҙОРФГюіцТ»ёц»ЖЙ«Ж№ЕТЗтәНТ»ёц°ЧЙ«Ж№ЕТЗтөДёЕВКЈ»
ЗуТ»ҙОРФГюіцТ»ёц»ЖЙ«Ж№ЕТЗтәНТ»ёц°ЧЙ«Ж№ЕТЗтөДёЕВКЈ»
![]() ЕР¶ПёГУОП·КЗ·с№«ЖҪЈҝІўЛөГчАнУЙЈ®
ЕР¶ПёГУОП·КЗ·с№«ЖҪЈҝІўЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com