练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，每个小方格都是边长为1的正方形，

    （1）求图中格点四边形ABCD的面积和周长；

    （2）求的度数．

    【答案】（1）面积为12.5；周长为；（2）90°

    【解析】

    （1）四边形ABCD的面积等于大正方形的面积减去4个直角三角形的面积；由勾股定理求出AD、AB、BC、CD，即可得出四边形ABCD的周长；
    （2）求出AD2+CD2=AC2，由勾股定理的逆定理即可求出结果．

    解：（1）根据题意得：
    四边形ABCD的面积=5×5-×3×3-×2×3-×2×4-×2×1=12.5；
    由勾股定理得：

    AD=，AB=，

    BC=，CD=，

    ∴四边形ABCD的周长==；

    （2）∵AD2+CD2=5+20=25，AC2=52=25，
    ∴AD2+CD2=AC2，
    ∴∠ADC=90°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】按规律填空．

    (1)1,3,5,7,9，__________；

    (2)2,5,8,11,14，__________；

    (3)，，，，__________；

    (4)，，，，__________；

    (5)2,6,15,31,56，__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了这15人某月的加工零件个数．（如下表）

    每人加工零件数

    54

    45

    30

    24

    21

    12

    人 数

    1

    1

    2

    6

    3

    2

    （1）写出这15人该月加工零件数的平均数、中位数和众数；

    （2）假设生产部负责人把每位工人的月加工零件数定为24件，你认为是否合理？为什么？如果不合理，请你设计一个较为合理的生产定额，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列函数中，当x＞0时，y的值随x的值增大而增大的是（ ）
    A.y=﹣x2
    B.y=x﹣1
    C.y=﹣x+1
    D.y=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图中折线表示芳芳骑自行车离家的距离与时间的关系，她9点离开家，15点回家，请根据图象回答下列问题：

    （1）芳芳到达离家最远的地方时，离家________千米；

    （2）第一次休息时离家________ 千米；

    （3）她在10：00~10：30的平均速度是_________；

    （4）芳芳一共休息了_________ 小时；

    （5）芳芳返回用了____________小时；

    （6）返回时的平均速度是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

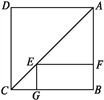
    【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.

    (1)求证:四边形BFEG是矩形;

    (2)求四边形EFBG的周长;

    (3)当AF的长为多少时,四边形BFEG是正方形?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，A（a，0），B（0，2）

    （1）点（k+1，2k﹣5）关于x轴的对称点在第一象限，a为实数k的范围内的最大整数，求A点的坐标及△AOB的面积；

    （2）在（1）的条件下如图1，点P是第一象限内的点，且△ABP是以AB为腰的等腰直角三角形，请直接写出P点坐标；

    （3）在（1）的条件下，如图2，以AB、OB的作等边△ABC和等边△OBD，连接AD、OC交于E点，连接BE．

    ①求证：EB平分∠CED；

    ②M点是y轴上一动点，求AM+CM最小时点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,抛物线y=ax2+bx+c的顶点为M（﹣2,﹣4），与x轴交于A、B两点,且A（﹣6,0），与y轴交于点C．

    （1）求抛物线的函数解析式；
    （2）求△ABC的面积；
    （3）能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大？若能,请求出点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，坐标原点O是菱形ABCD的对称中心．边AB与x轴平行，点B（1，-2），反比例函数 （k≠0）的图象经过A，C两点．

    （1）求点C的坐标及反比例函数的解析式．
    （2）直线BC与反比例函数图象的另一交点为E，求以O，C，E为顶点的三角形的面积．

    查看答案和解析>>

    同步练习册答案