
 ��ͼ��ʾ������ABCD�����߳�AB=18cm��AD=4cm����P��Q�ֱ��A��Bͬʱ��������P�ڱ�AB������AB������2cm/s���ٶ������˶�����Q�ڱ�BC������BC������1cm/s���ٶ������˶���������һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶������˶�ʱ��Ϊxs����PBQ�����Ϊy��cm2����
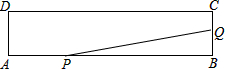
��ͼ��ʾ������ABCD�����߳�AB=18cm��AD=4cm����P��Q�ֱ��A��Bͬʱ��������P�ڱ�AB������AB������2cm/s���ٶ������˶�����Q�ڱ�BC������BC������1cm/s���ٶ������˶���������һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶������˶�ʱ��Ϊxs����PBQ�����Ϊy��cm2�������� ��1����������ó�AP=2xcm��BQ=xcm���ó�BP=18-2x��cm������PBQ�����=$\frac{1}{2}$BQ•BP�����ɵó������
��2���Ѷ��κ��������䷽�����ʽ�����ɵó������
��� �⣺��1����������ã���B=90�㣬BC=AD=4cm��AP=2xcm��BQ=xcm��
��BP=18-2x��cm����
���PBQ�����=$\frac{1}{2}$BQ•BP=$\frac{1}{2}$x��18-2x��=-x2+9x��
��y=-x2+9x��
x��ȡֵ��Χ��0��x��4��
��2���˶�4s���PBQ����������������20cm2���������£�
��y=-x2+9x
=-��x-4.5��2+20.25��
-1��0��
��y�����ֵ��
��x=4.5ʱ��
y�����ֵΪ20.25��
�֡�x��4��
�൱x=4ʱ��y�õ����ֵ=-42+9��4=20��
���˶�4s���PBQ����������������20cm2��
���� ���⿼���˾��ε����ʡ�����������ļ��㷽�������κ�������ֵ���������վ��ε����ʣ����ܽ������������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+a3=a4 | B�� | ��a+b��2=a2+b2 | C�� | a10��a2=a5 | D�� | ��a2��3=a6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽�һ����װʳƷ�Ƿ��з����� | |
| B�� | �˽�ij��ѧ����50���ܡ��ijɼ� | |
| C�� | �����ҹ����������������Ⱦ�����Ŀ��� | |
| D�� | �˽�һ�����ݵ�ʹ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
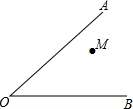 ��ͼ��ʾ��M�ǡ�AOB��-�㣮
��ͼ��ʾ��M�ǡ�AOB��-�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com