
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
| 与标准质量的差值(单位:g) | -5 | -2 | 0 | 1 | 3 | 5 |
| 袋数 | 1 | 4 | 2 | 4 | 5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 甲班人数(人) | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙班人数(人) | 4 | 4 | 16 | 2 | 12 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
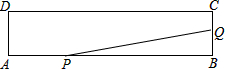 如图所示,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB边上沿AB方向以2cm/s的速度匀速运动,点Q在边BC边上沿BC方向以1cm/s的速度匀速运动,当其中一个点停止运动时,另一个点也停止运动,设运动时间为xs,△PBQ的面积为y(cm2).
如图所示,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB边上沿AB方向以2cm/s的速度匀速运动,点Q在边BC边上沿BC方向以1cm/s的速度匀速运动,当其中一个点停止运动时,另一个点也停止运动,设运动时间为xs,△PBQ的面积为y(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
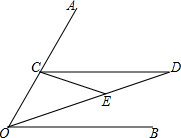 已知∠AOB,点C是OA上任意一点,CD∥OB,且∠AOE=∠CEO,∠DCE=∠D,试说明∠DOB=$\frac{1}{3}$∠AOB.
已知∠AOB,点C是OA上任意一点,CD∥OB,且∠AOE=∠CEO,∠DCE=∠D,试说明∠DOB=$\frac{1}{3}$∠AOB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com