
 如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )
如图,在△ABC中,∠C=90°,AC=18,BC=20,若有一半径为9的圆分别与AC和BC相切,则下列可找到此圆圆心的方法是( )| A. | BC的垂直平分线与AC的垂直平分线的交点 | |
| B. | ∠C的平分线与BC的垂直平分线的交点 | |
| C. | ∠C的平分线与AC的垂直平分线的交点 | |
| D. | ∠C的平分线与AB的垂直平分线的交点 |
分析 由圆O分别与AC和BC相切,根据切线的性质得到圆心O到AC和BC的距离都等于半径,根据到角的两边距离相等的点在角的平分线上,可得出圆心O一定在∠C的角平分线上,因为圆的半径为9,圆心到AC的距离为9,又AC=18且∠C=90°,得到AC的中垂线上的点到AB的距离为9,进而得到∠V的角平分线与AC的中垂线的交点即为圆心O,即可得到正确的选项.
解答 解:如图所示:
∵圆O分别与AC和BC相切,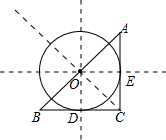
∴OE=OD=r,且OE⊥AC,OD⊥BC,
∴圆心O在∠ACB的角平分线上,
∵OE=r=9,AC=18,且∠ACB=90°,
∴AC的中垂线上的点到BC的距离为9,
∴∠C的角平分线与AC的中垂线的交点即为圆心0.
故选C.
点评 此题考查了切线的性质,角平分线的判定与性质,以及平行线的性质,熟练掌握切线的性质是解本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
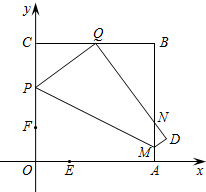 如图,四边形OABC为正方形,点A在x轴上,点C在y轴上,点B(8,8),点P在边OC上,点M在边AB上.把四边形OAMP沿PM对折,PM为折痕,使点O落在BC边上的点Q处.动点E从点O出发,沿OA边以每秒1个单位长度的速度向终点A运动,运动时间为t,同时动点F从点O出发,沿OC边以相同的速度向终点C运动,当点E到达点A时,E、F同时停止运动.
如图,四边形OABC为正方形,点A在x轴上,点C在y轴上,点B(8,8),点P在边OC上,点M在边AB上.把四边形OAMP沿PM对折,PM为折痕,使点O落在BC边上的点Q处.动点E从点O出发,沿OA边以每秒1个单位长度的速度向终点A运动,运动时间为t,同时动点F从点O出发,沿OC边以相同的速度向终点C运动,当点E到达点A时,E、F同时停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
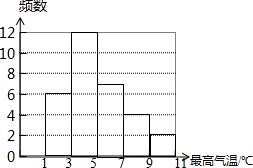 根据石家庄2014年1月份全月的各天最高气温(℃)记录,绘制出如图所示的频数分布直方图(图中分组含量低值,不含最高值),由图中信息可知,最高气温达到5℃及其以上的有13天.
根据石家庄2014年1月份全月的各天最高气温(℃)记录,绘制出如图所示的频数分布直方图(图中分组含量低值,不含最高值),由图中信息可知,最高气温达到5℃及其以上的有13天.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com