Question

9．（1）如图1，△ABC中，∠C=90°，AB的垂直平分线交AC于点D，连接BD．若AC=2，BC=1，则△BCD的周长为3；
（2）O为正方形ABCD的中心，E为CD边上一点，F为AD边上一点，且△EDF的周长等于AD的长．
①在图2中求作△EDF（要求：尺规作图，不写作法，保留作图痕迹）；
②在图3中补全图形，求∠EOF的度数；
③若$\frac{AF}{CE}=\frac{8}{9}$，则$\frac{OF}{OE}$的值为$\frac{2\sqrt{2}}{3}$．

Answer 1

分析 （1）由线段垂直平分线的性质得出BD=AD，得出△BCD的周长=BC+CD+BD=BC+AC，即可得出结果；
（2）①在AD上截取AH=DE，再作EH的垂直平分线，交AD于F，△EDF即为所求；
②连接OA、OD、OH，由正方形的性质得出∠1=∠2=45°，由SAS证明△ODE≌△OAH，得出∠DOE=∠AOH，OE=OH，得出∠EOH=90°，证出EF=HF，由SSS证明△EOF≌△HOF，得出∠EOF=∠HOF=45°即可；
③作OG⊥CD于G，OK⊥AD于K，设AF=8t，则CE=9t，设OG=m，由正方形的性质得出GE=CE-CG=9t-m，DE=2CG-CE=2m-9t，FK=AF-KA=8t-m，DF=2DK-AF=2m-8t，由HL证明Rt△EOG≌Rt△HOK，得出GE=KH，因此EF=GE+FK=17t-2m，由勾股定理得出方程，解方程求出m=6t，得出OG=OK=6t，GE=9t-m=9t-6t=3t，FK=8t-m=2t，由勾股定理即可得出结果．

解答 解：（1）∵AB的垂直平分线交AC于点D，
∴BD=AD，
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3，
故答案为：3； 
（2）①如图1所示：
△EDF即为所求； 
②如图2所示：AH=DE，
连接OA、OD、OH，
∵点O为正方形ABCD的中心，
∴OA=OD，∠AOD=90°，∠1=∠2=45°，
在△ODE和△OAH中，
$\left\{\begin{array}{l}{OA=OD}\\{∠2=∠1}\\{AH=DE}\end{array}\right.$，
∴△ODE≌△OAH（SAS），
∴∠DOE=∠AOH，OE=OH，
∴∠EOH=90°，
∵△EDF的周长等于AD的长，
∴EF=HF，
在△EOF和△HOF中，
$\left\{\begin{array}{l}{OE=OH}\\{OF=OF}\\{EF=HF}\end{array}\right.$，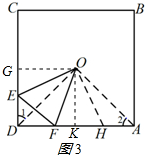
∴△EOF≌△HOF（SSS），
∴∠EOF=∠HOF=45°；
③作OG⊥CD于G，OK⊥AD于K，如图3所示：
设AF=8t，则CE=9t，设OG=m，
∵O为正方形ABCD的中心，
∴四边形OGDK为正方形，CG=DG=DK=KA=$\frac{1}{2}$AB=OG，
∴GE=CE-CG=9t-m，DE=2CG-CE=2m-9t，FK=AF-KA=8t-m，DF=2DK-AF=2m-8t，
由（2）②知△EOF≌△HOF，
∴OE=OH，EF=FH，
在Rt△EOG和Rt△HOK中，
$\left\{\begin{array}{l}{OE=OH}\\{OG=OK}\end{array}\right.$，
∴Rt△EOG≌Rt△HOK（HL），
∴GE=KH，
∴EF=GE+FK=9t-m+8t-m=17t-2m，
由勾股定理得：DE²+DF²=EF²，
∴（2m-9t）²+（2m-8t）²=（17t-2m）²，
整理得：（m+6t）（m-6t）=0，
∴m=6t，
∴OG=OK=6t，GE=9t-m=9t-6t=3t，FK=8t-m=2t，
∴$\frac{OF}{OE}$=$\frac{\sqrt{O{K}^{2}+F{K}^{2}}}{\sqrt{O{G}^{2}+G{E}^{2}}}$=$\frac{\sqrt{36{t}^{2}+4{t}^{2}}}{\sqrt{36{t}^{2}+9{t}^{2}}}$=$\sqrt{\frac{40}{45}}$=$\frac{2\sqrt{2}}{3}$．
故答案为$\frac{2\sqrt{2}}{3}$．

点评 本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、线段垂直平分线的性质、勾股定理、解方程等知识；本题综合性强，有一定难度，熟练掌握正方形的性质，证明三角形全等是解决问题的关键．