
 如图,小亮以0.5m/s的速度从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,从开始到停止共所需时间为480s.
如图,小亮以0.5m/s的速度从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,从开始到停止共所需时间为480s.  优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
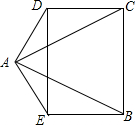 如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.
如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和点D(5,0).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和点D(5,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E是正方形ABCD内一点,点E到点A,B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$.将△ADE绕点A旋转至△ABG,连结ABG,连结AE,并延长AE与BC相交于点F,连接GF,则线段GF长为$\frac{\sqrt{178}}{3}$.
如图,点E是正方形ABCD内一点,点E到点A,B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$.将△ADE绕点A旋转至△ABG,连结ABG,连结AE,并延长AE与BC相交于点F,连接GF,则线段GF长为$\frac{\sqrt{178}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
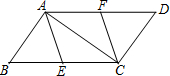 已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.
已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com