
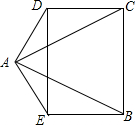
 如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.
如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.分析 (1)借助已有的条件先证明△ADC≌△AEB,得出DC=EB,从而断定四边形DEBC为平行四边形,再由边角关系去证明∠EDC=90°即可得出结论;
(2)作辅助线AN∥CD,由于△ABC是等边三角形,从而可以得出直角三角形AMD中的两直角边,根据勾股定理即可求得;
(3)巧妙的假设总清扫量为1,由已知即可找到规定的时间.
解答 (1)证明:∠DAB=∠DAC+∠BAC,∠EAC=∠EAB+∠BAC,
∵∠DAB=∠EAC,
∴∠DAC=∠EAB,
在△DAC与△EAB中,
有$\left\{\begin{array}{l}{AB=AC}\\{∠DAC=∠EAB}\\{AD=AE}\end{array}\right.$,
∴△ADC≌△AEB(SAS),
∴DC=EB,∠ADC=∠AEB,
∵DE=CB,
∴四边形DEBC是平行四边形(两组对边相等),
∵AD=AE,
∴∠ADE=∠AED,
又∵∠ADC=∠AEB,且∠EDC=∠ADC-∠ADE,∠DEB=∠AEB-∠AED,
∴∠EDC=∠DEB,
∵四边形DEBC是平行四边形,
∴∠EDC+∠DEB=180°(平行四边形同旁内角互补),
∴∠EDC=∠DEB=90°,
∴四边形DEBC是矩形.
证毕.
(2)解:过点A做AN∥CD,交DE于M点,交BC于N点,如图:
∵四边形DEBC是矩形,AM∥CD,
∴AM⊥DE,AN⊥BC,DM=CN,
∵△ABC是等边三角形,BC=4,
∴CN=$\frac{1}{2}$BC=2,AB=AC=BC=4,
∴AN=$\sqrt{A{C}^{2}-C{N}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵CD=BE=MN=2,AM=AN-MN,
∴AM=2$\sqrt{3}$-2,
由AM⊥DE可知:AD2=AM2+DM2=AM2+CN2=20-8$\sqrt{3}$,
答:AD2的值为20-8$\sqrt{3}$.
(3)解:设该班的清洁区总工作量为1,那么李拼每分钟打扫$\frac{1}{12}$、张博每分钟打扫$\frac{1}{15}$,
由题意可知打扫时间为6+(1-$\frac{1}{15}$×6)÷($\frac{1}{12}$+$\frac{1}{15}$)=6+$\frac{9}{15}$÷$\frac{9}{60}$=6+4=10(分钟),
故规定的时间为10分钟.
点评 本题考查到了矩形的判定定理,勾股定理,等边三角形三线合一问题已经巧设方程,解题的关键是结合图形,熟练的利用各大定理.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:填空题
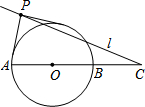 如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°.
如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小亮以0.5m/s的速度从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,从开始到停止共所需时间为480s.
如图,小亮以0.5m/s的速度从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,从开始到停止共所需时间为480s.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为A、B.
如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA、PB,切点分别为A、B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com