
 如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.分析 (1)表示出PH,然后分①当AP=AD时,②当AD=PD时,根据等腰三角形三线合一的性质,AH=PH,列式进行计算即可得解;③当AP=PD时,表示出PH,然后在Rt△DPH中,根据勾股定理列式进行计算即可得解;
(2)根据同角的余角相等求出∠HDP=∠EPB,再根据两角对应相等,两三角形相似求出△DPH和△PEB相似,然后根据相似三角形对应边成比例列出比例式整理即可得解;
(3)根据PQ过点C时,BE=4,代入(2)的BE的表达式,再根据一元二次方程的解确定即可.
解答 解:(1)过D点作DH⊥AB于H,则四边形DHBC为矩形,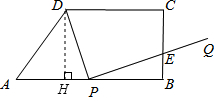
∴DH=BC=4,HB=CD=6,
∴AH=2,AD=2$\sqrt{5}$,
∵AP=x,
∴PH=x-2,
情况①:当AP=AD时,即x=2$\sqrt{5}$,
情况②:当AD=PD时,则AH=PH,
∴2=x-2,
解得x=4,
情况③:当AP=PD时,则Rt△DPH中,x2=42+(x-2)2,
解得x=5,
∵2<x<8,
∴当x为2$\sqrt{5}$、4、5时,△APD是等腰三角形;
(2)∵∠DPE=∠DHP=90°,
∴∠DPH+∠EPB=∠DPH+∠HDP=90°,
∴∠HDP=∠EPB,
又∵∠DHP=∠B=90°,
∴△DPH∽△PEB,
∴$\frac{DH}{PH}=\frac{PB}{EB}$,
∴$\frac{4}{x-2}=\frac{8-x}{y}$,
整理得:$y=\frac{1}{4}(x-2)(8-x)=-\frac{1}{4}{x^2}+\frac{5}{2}x-4$;
(3)存在,
由(2)得△DPH∽△PEB,
∴$\frac{a}{8-x}=\frac{x-2}{y}$,
∴y=$\frac{{({8-x})({x-2})}}{a}$,
当y=a时,(8-x)(x-2)=a2,即x2-10x+(16+a2)=0,△=100-4(16+a2)≥0,
即100-64-4a2≥0,
即a2≤9,
又∵a>0,
∴0<a≤3,
∴当BC满足0<BC≤3时,存在点P,使得PQ经过C,
此时,AP的长为$x=\frac{{10±\sqrt{100-4(16+{a^2})}}}{2}=5±\sqrt{9-{a^2}}$.
点评 本题考查了四边形综合题,主要考查了直角梯形的性质,勾股定理,等腰三角形的性质,相似三角形的判定与性质,一元二次方程的解的情况,综合性较强,难度较大,(1)要根据等腰三角形的腰长的不同分情况讨论.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P.
如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
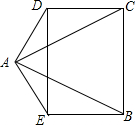 如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.
如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E是正方形ABCD内一点,点E到点A,B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$.将△ADE绕点A旋转至△ABG,连结ABG,连结AE,并延长AE与BC相交于点F,连接GF,则线段GF长为$\frac{\sqrt{178}}{3}$.
如图,点E是正方形ABCD内一点,点E到点A,B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$.将△ADE绕点A旋转至△ABG,连结ABG,连结AE,并延长AE与BC相交于点F,连接GF,则线段GF长为$\frac{\sqrt{178}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com