练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．先化简，再求值：（x-4）（x+4y）+（3x-4y）2，其中x=2，y=-1．

    分析 本题应对代数式去括号，合并同类项，从而将整式化为最简形式，然后把x、y的值代入即可．

    解答 解：（x-4）（x+4y）+（3x-4y）2，
    =x2+4xy-4x-16y+9x2-24xy+16y2
    =10x2-20xy-4x-16y+16y2，
    把x=2，y=-1代入10x2-20xy-4x-16y+16y2=40+40-8+16+16=104．

    点评 本题考查了整式的化简，整式的混合运算实际上就是去括号、合并同类项，这是各地中考的常考点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．在△ABC中∠C=90°，c=100，a：b=3：4，则a=60，b=80．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

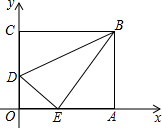    17．如图所示，把矩形OABC放入平面直角坐标系中，点B坐标为（10，8），点D是OC上一动点，将矩形OABC沿直线BD折叠，点C恰好落在OA上的点E处，则点D的坐标是（　　）
    A．（0，4）B．（0，5）C．（0，3）D．（3，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，已知数轴上点A表示的数为6，点B表示的数为-4，C为线段AB的中点，动点P从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t＞0）秒．
    （1）点C表示的数是1；
    （2）当t=5秒时，点P到达点A处；
    （3）点P表示的数是2t-4（用含字母t的代数式表示）；
    （4）当t=1.5秒或3.5秒秒时，线段PC的长为2个单位长度；
    （5）若动点Q同时从点A出发，以每秒1个单位长度的速度沿数轴向左匀速运动，那么，当t=3秒或$\frac{11}{3}$秒秒时，PQ的长为1个单位长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．在平面直角坐标系中，已知点A（1，2），B（4，5），C（5，2），如果存在点E，使△ACE和△ACB全等，则符合题意的点共有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．大庆素有百湖之城的美称，如图所示．在临湖高出水面50米的塔AB顶层A处望见一艘飞艇停留在平静的湖面上空某处．观察到艇底部醒目标志阳目志P处的仰角为45°，又观察到其在湖中的影像的俯角为60°，试求飞艇距湖面的高度h（结果可用含根号的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，该表面展开图按虚线折叠成正方体后，相对面上的两个数互为相反数，则（x+y）的值为（　　）
    A．-2B．-3C．2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．三个全等的直角梯形①、②、③在平面直角坐标系中的位置如图所示，抛物线y=ax2+bx+c经过梯形的顶点A、B、C、D，已知梯形的两条底边长分别为4，6，则梯形的两腰长分别为2、2$\sqrt{2}$，该抛物线解析式为y=$-\frac{1}{4}{x}^{2}+\frac{1}{2}x+6$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

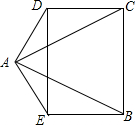    2．如图，AB=AC，AD=AE，∠DAB=∠EAC，DE=CB．
    （1）求证：四边形DEBC是矩形．
    （2）若△ABC是等边三角形，BC=4，EB=2，求AD2的值．
    （3）某班的清洁区形如五边形ADCBE，值日生李拼、张博两人必须在规定时间内打扫完毕，若李拼单独完成需12分钟，张博单独完成需15分钟．张博打扫6分钟后，李拼加入一起打扫，两人恰好在规定时间内完成，求规定时间．

    查看答案和解析>>

    同步练习册答案