
 大庆素有百湖之城的美称,如图所示.在临湖高出水面50米的塔AB顶层A处望见一艘飞艇停留在平静的湖面上空某处.观察到艇底部醒目标志阳目志P处的仰角为45°,又观察到其在湖中的影像的俯角为60°,试求飞艇距湖面的高度h(结果可用含根号的式子表示).
大庆素有百湖之城的美称,如图所示.在临湖高出水面50米的塔AB顶层A处望见一艘飞艇停留在平静的湖面上空某处.观察到艇底部醒目标志阳目志P处的仰角为45°,又观察到其在湖中的影像的俯角为60°,试求飞艇距湖面的高度h(结果可用含根号的式子表示). 分析 设AC=x,则PC=AC=x,根据山顶A处高出水面50m,得出DC=50,DP′=x+50,根据∠P′AC=60°,得出P′C=$\sqrt{3}$x,DP′=$\sqrt{3}$x-50,从而列出方程,求出x的值,即可求得飞艇距湖面的高度h.
解答 解:点P在湖中的影像为P′,如右图所示,
设AC=xm,
在Rt△ACP中∠PAC=45°,则∠P=45°,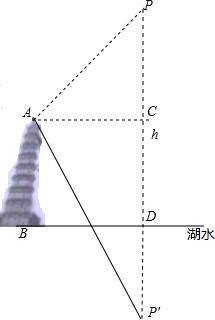
所以PC=AC=x,
∵山顶A处高出水面50m,
∴DC=50,
∴DP′=DP=PC+DC=x+50,
∵∠P′AC=60°,
∴P′C=tan60°•AC=$\sqrt{3}$x,
∴DP′=P′C-DC=$\sqrt{3}$x-50,
∴x+50=$\sqrt{3}$x-50,
x=50($\sqrt{3}$+1),
∴h=PD=50$\sqrt{3}$+100,
答:飞艇离湖面的高度是(50$\sqrt{3}$+100)m.
点评 本题考查了解直角三角形的应用-仰角俯角问题,解题的关键是能借助俯角、仰角构造直角三角形并根据数形结合的思想利用三角函数解直角三角形.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
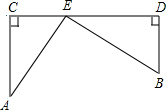 如图所示,在铁路线CD同侧有两个村庄A,B,它们到铁路线的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25,现在要在铁路旁建一个农副产品收购站E,使A,B两村庄到收购站的距离相等,用你学过的知识,通过计算,确定点E的位置.
如图所示,在铁路线CD同侧有两个村庄A,B,它们到铁路线的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25,现在要在铁路旁建一个农副产品收购站E,使A,B两村庄到收购站的距离相等,用你学过的知识,通过计算,确定点E的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
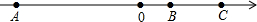 如图:已知A、B、C是数轴上的三点,点C表示的数是6,BC=4,AB=12,
如图:已知A、B、C是数轴上的三点,点C表示的数是6,BC=4,AB=12,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1≤k≤1 | B. | 0<k≤1 | C. | k≤1 | D. | k≤-1或k≥1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com