练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，梯形ABCD中，AD//BC，对角线AC、BD相交于点O ，若,则等于（）

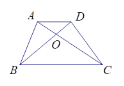
    A. 1：6B. 1：3C. 1：4D. 1：5

    【答案】C

    【解析】

    由AD与BC平行，利用两直线平行得到两对内错角相等，利用两对角相等的三角形相似得到三角形AOD与三角形BOC相似，由三角形AOD与三角形ACD面积之比求出三角形AOD与三角形COD面积之比，进而得出OA与OC之比，利用相似三角形面积之比等于相似比的平方即可求出所求面积之比．

    解：∵AD∥BC，
    ∴∠DAC=∠ACB，∠ADB=∠DBC，
    ∴△AOD∽△COB，
    ∵S△AOD：S△ACD=1：3，
    ∴S△AOD：S△DOC=1：2，即OA：OC=1：2，
    ∴S△AOD：S△BOC=1：4，
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ΔABC中，AB=AC,若将ΔABC绕点C顺时针180得到ΔFEC。

    （1）试猜想AE与BF有何关系，并说明理由；

    （2）若ΔABC的面积为3cm2,求四边形ABFE的面积;

    (3)当∠ACB为多少度时，四边形ABFE为矩形？说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

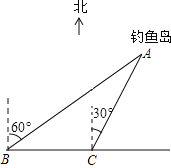
    【题目】如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行多少海里与钓鱼岛A的距离最近？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD为⊙O的直径，弦AB⊥CD，垂足为E，，CE=1，AB=6，则弦AF的长度为___.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校需要添置教师办公桌椅A、B两型共200套，已知2套A型桌椅和1套B型桌椅共需2000元，1套A型桌椅和3套B型桌椅共需3000元．

    （1）求A，B两型桌椅的单价；

    （2）若需要A型桌椅不少于120套，B型桌椅不少于70套，平均每套桌椅需要运费10元．设购买A型桌椅x套时，总费用为y元，求y与x的函数关系式，并直接写出x的取值范围；

    （3）求出总费用最少的购置方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：关于x的方程

    （1）求证：不论m取何值时，方程总有两个不相等的实数根

    （2）若方程的一个根为1，求m的值及方程的另一根

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知矩形AOCB，AB=6cm，BC=16cm，动点P从点A出发，以3cm/s的速度向点O运动，直到点O为止；动点Q同时从点C出发，以2cm/s的速度向点B运动，与点P同时结束运动．

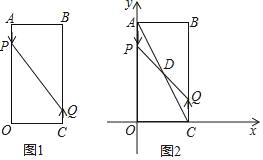
    （1）当运动时间为2s时，P、Q两点的距离为　 　cm；

    （2）请你计算出发多久时，点P和点Q之间的距离是10cm；

    （3）如图2，以点O为坐标原点，OC所在直线为x轴，OA所在直线为y轴，1cm长为单位长度建立平面直角坐标系，连结AC，与PQ相交于点D，若双曲线过点D，问k的值是否会变化？若会变化，说明理由；若不会变化，请求出k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，对于点和点，给出如下定义：若，则称点为点的限变点．例如：点的限变点的坐标是，点的限变点的坐标是．

    （1）①点的限变点的坐标是___________；

    ②在点，中有一个点是函数图象上某一个点的限变点，这个点是_______________；

    （2）若点在函数的图象上，其限变点的纵坐标的取值范围是，求的取值范围；

    （3）若点在关于的二次函数的图象上，其限变点的纵坐标的取值范围是或，其中．令，求关于的函数解析式及的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形网格上有A、B、O三点，如果用（3，3）表示方格纸上A点的位置，（1，1）表示B点的位置，O点也在网格点上．

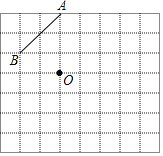
    （1）作出点B关于直线OA的轴对称点C，写出点C坐标．（不写作法，但要在图中标出字母）；

    （2）作出△ABC关于点O的中心对称图形△A′B′C′，写出A′、B′、C′三点的坐标；（不写作法，但要标出字母）；

    （3）若网格上的最小正方形边长为1，求出△A′B′C′的面积．

    查看答案和解析>>

    同步练习册答案