
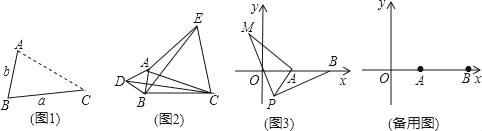
����Ŀ����1�����֣���ͼ1����AΪ�߶�BC��һ���㣬��BC��a��AB��b�һش𣺵���Aλ�������߶ε��ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ���٣��ú�a��b��ʽ�ӱ�ʾ����
��2��Ӧ�ã���AΪ�߶�BC��һ���㣬��BC��4��AB��2����ͼ2��ʾ���ֱ���AB��ACΪ�ߣ����ȱ�������ABD�͵ȱ�������ACE������CD��BE�������ҳ�ͼ����BE��ȵ��߶Σ���˵�����ɣ���ֱ��д���߶�BE�������ֵ��
��3����չ����ͼ3����ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��5��0������PΪ�߶�AB��һ���㣬��PA��2��PM��PB����BPM��90�㣬��ֱ��д���߶�AM�������ֵ����ʱ��P�����꣮
���𰸡���1��CB��a+b����2����CD��BE�����ɼ������������ֵΪ4����3�����������ĵ�P���꣨2��![]() ��
��![]() ����2��
����2��![]() ����
����![]() ����AM�����ֵΪ2
����AM�����ֵΪ2![]() +3��
+3��
��������
��1�����ݵ�Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�����ɵõ�����
��2�������ݵȱ������ε����ʵõ�AD=AB��AC=AE����BAD=��CAE=60�����Ƴ���CAD�ա�EAB������ȫ�������ε����ʵõ�CD=BE���������߶�BE�������ֵ=�߶�CD�����ֵ�����ݣ�1���еĽ��ۼ��ɵõ������
��3������BM������APM���ŵ�P˳ʱ����ת90���õ���PBN������AN���õ���APN�ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�PN=PA=2��BN=AM�����ݵ�N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ�����ɵõ����ֵΪ2![]() +3����P��PE��x����E�����ݵ���ֱ�������ε����ʣ����ɵõ�P���һ�����꣬�ٸ��ݶԳ��Եõ�P�������һ�����꼴�ɵó���
+3����P��PE��x����E�����ݵ���ֱ�������ε����ʣ����ɵõ�P���һ�����꣬�ٸ��ݶԳ��Եõ�P�������һ�����꼴�ɵó���
��1���ߵ�AΪ�߶�BC��һ���㣬��BC��a��AB��b��
�൱��Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪBC+AB��a+b��
��2����CD��BE��
���ɣ��ߡ�ABD���ACE�ǵȱ������Σ�
��AD��AB��AC��AE����BAD����CAE��60�㣬
���BAD+��BAC����CAE+��BAC��
����CAD����EAB��
�ڡ�CAD���EAB�У�
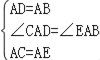 ��
��
���CAD�ա�EAB��
��CD��BE��
�����߶�BE�������ֵ���߶�CD�����ֵ��
�ɣ�1��֪�����߶�CD�ij�ȡ�����ֵʱ����D��CB���ӳ����ϣ�
�����ֵΪBD+BC��AB+BC��4��
��3������BM���߽���APM���ŵ�P˳ʱ����ת90��õ���PBN������AN��

���APN�ǵ���ֱ�������Σ�
��PN��PA��2��BN��AM��
��A��������2��0������B��������5��0����
��OA��2��OB��5��
��AB��3��
���߶�AM�������ֵ���߶�BN�������ֵ��
�൱N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ��
���ֵ��AB+AN��
��AN��![]() AP��2
AP��2![]() ��
��
�����ֵΪ2 ![]() +3��
+3��
��ͼ2����P��PE��x����E��

�ߡ�APN�ǵ���ֱ�������Σ�
��PE��AE��![]() ��
��
��OE��BO��AB��AE��5��3��![]() ��2��
��2��![]() ��
��
��P��2��![]() ��
��![]() ����
����
��ͼ3�У�
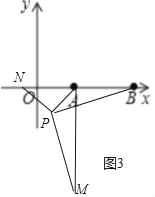
���ݶԳ��Կ�֪����P�ڵ�������ʱ��P��2��![]() ����
����![]() ��ʱ��Ҳ����������
��ʱ��Ҳ����������
�������������������ĵ�P���꣨2��![]() ��
��![]() ����2��
����2��![]() ����
����![]() ����AM�����ֵΪ2
����AM�����ֵΪ2![]() +3��
+3��


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
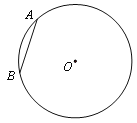
����Ŀ����ͼ���ڰ뾶Ϊ2�ġ�O�У���AB��2����O�ϴ��ڵ�C����AC��2![]() �����BAC�Ķ���Ϊ___.
�����BAC�Ķ���Ϊ___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
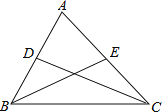
����Ŀ����ͼ����֪![]() �У��ӳ�
�У��ӳ�![]() ���ϵ�����
���ϵ�����![]() ��
��![]() ��ʹ
��ʹ![]() ���ӳ�
���ӳ�![]() ���ϵ�����
���ϵ�����![]() ��
��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��
��1����ȫͼ�Σ�
��2��![]() �Ĵ�С��ϵ��Σ�֤����Ľ��ۣ�
�Ĵ�С��ϵ��Σ�֤����Ľ��ۣ�
��3��![]() �����λ�ù�ϵ��Σ�֤����Ľ��ۣ�
�����λ�ù�ϵ��Σ�֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪m��n��m<n���ǹ���x�ķ��̣�x�Ca����x�Cb��=2����������a<b���������ж���ȷ����
A. a<m<b<n B. m<a<n<b
C. a<m<n<d D. m<a<b<n
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
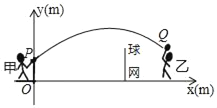
����Ŀ���ס������˽�����ë����������ɵ㣬����е�·��Ϊ�����ߵ�һ���֣���ͼ����ƽ��ֱ������ϵ������O�����Ϸ�1m��P��������ë����еĸ߶�y��m������ë������վ��λ�ã���O����ˮƽ����x��m��֮�����㺯�ܱ���ʽy��a��x��4��2+h����֪��O��������ˮƽ����Ϊ5m�������ĸ߶�Ϊ1.55m���߽���O��ˮƽ����Ϊ10m��
��1����a����![]() ʱ����h��ֵ����ͨ�������жϴ����ܷ������
ʱ����h��ֵ����ͨ�������жϴ����ܷ������
��2�������������������һ�������ˮƽ����lm����������û�гɹ������ھ�����ˮƽ����lm�������߶�2.2m���ɹ���ͨ�������жϴ�������磿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ��������������У���![]() ������ijĿ�굺��
������ijĿ�굺��![]() �ڱ�ƫ��
�ڱ�ƫ��![]() ���������Ϻ���
���������Ϻ���![]() ���ﵽ
���ﵽ![]() �����������췽�����˱�ƫ��
�����������췽�����˱�ƫ��![]() �����ִ����ֺ��еķ���������Ŀ�굺����������Ƕ��٣��������ȷ��
�����ִ����ֺ��еķ���������Ŀ�굺����������Ƕ��٣��������ȷ��![]() ����ο����ݣ�
����ο����ݣ�![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C=90����AD�ǽ�ƽ���ߣ�EΪAC���ϵĵ㣬DE=DB�����н��ۣ��١�DEA����B=180������ ��CDE=��CAB���� AC=![]() (AB��AE)���� S��ADC=
(AB��AE)���� S��ADC=![]() S�ı���ABDE��������ȷ�Ľ��۸���Ϊ( )
S�ı���ABDE��������ȷ�Ľ��۸���Ϊ( )
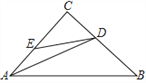
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
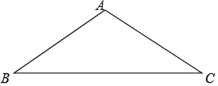
����Ŀ����ͼ����ABC�У�AB��AC����A��108�㣮
��1��ʵ�����������AB�Ĵ�ֱƽ����DE����AB��BC�ֱ��ڵ�D��E���ó߹���ͼ��������ͼ�ۼ�����Ҫ��д������
��2����������㣺���AEC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����DΪ�����������y=��x2+bx+c��x����A��B���㣬��y���ڵ�C��ֱ��BC�ı���ʽΪy=��x+3��
��1���������ߵı���ʽ��
��2����ֱ��BC����һ��P��ʹPO+PA��ֵ��С�����P�����ꣻ
��3����x�����Ƿ����һ��Q��ʹ����A��C��QΪ��������������BCD���ƣ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com