Question

【题目】如图，在等边三角形ABC右侧作射线CP，∠ACP=（0°<<60°），点A关于射线CP的对称点为点D，BD交CP于点E，连接AD，AE.

（1）求∠DBC的大小（用含的代数式表示）；

（2）在（0°<<60°）的变化过程中，∠AEB的大小是否发生变化？如果发生变化，请直接写出变化的范围；如果不发生变化，请直接写出∠AEB的大小；

（3）用等式表示线段AE，BD，CE之间的数量关系，并证明.

Answer 1

【答案】（1）∠DBC；（2）∠AEB的大小不会发生变化，且∠AEB=60°；（3）BD=2AE+CE，证明见解析.

【解析】

（1）如图1，连接CD，由轴对称的性质可得AC=DC，∠DCP=∠ACP=，由△ABC是等边三角形可得AC=BC，∠ACB=60°，进一步即得∠BCD=，BC=DC，然后利用三角形的内角和定理即可求出结果；

（2）设AC、BD相交于点H，如图2，由轴对称的性质可证明△ACE≌△DCE，可得∠CAE=∠CDE，进而得∠DBC=∠CAE，然后根据三角形的内角和可得∠AEB=∠BCA，即可作出判断；

（3）如图3，在BD上取一点M，使得CM=CE，先利用三角形的外角性质得出∠BEC，进而得△CME是等边三角形，可得∠MCE=60°，ME=CE，然后利用角的和差关系可得∠BCM=∠DCE，再根据SAS证明△BCM≌△DCE，于是BM=DE，进一步即可得出线段AE，BD，CE之间的数量关系.

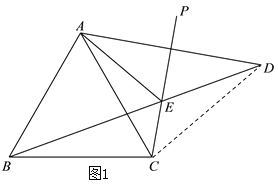
解：（1）如图1，连接CD，∵点A关于射线CP的对称点为点D，∴AC=DC，∠DCP=∠ACP=，

∵△ABC是等边三角形，∴AC=BC，∠ACB=60°，

∴∠BCD=，BC=DC，

∴∠DBC=∠BDC；

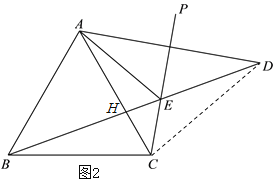
（2）∠AEB的大小不会发生变化，且∠AEB=60°.

理由：设AC、BD相交于点H，如图2，∵点A关于射线CP的对称点为点D，

∴AC=DC，AE=DE，又∵CE=CE，∴△ACE≌△DCE（SSS），∴∠CAE=∠CDE，

∵∠DBC=∠BDC，∴∠DBC=∠CAE，又∵∠BHC=∠AHE，∴∠AEB=∠BCA=60°，

即∠AEB的大小不会发生变化，且∠AEB=60°；

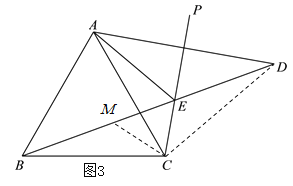
（3）AE，BD，CE之间的数量关系是：BD=2AE+CE.

证明：如图3，在BD上取一点M，使得CM=CE，

∵∠BEC=∠BDC+∠DCE=，

∴△CME是等边三角形，∴∠MCE=60°，ME=CE，

∴，

∴∠BCM=∠DCE，又∵BC=DC，CM=CE，

∴△BCM≌△DCE（SAS），∴BM=DE，

∵AE=DE，

∴BD=BM+ME+DE=2DE+ME=2AE+CE.