
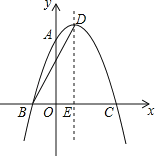
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长;
(3)点F在抛物线上运动,是否存在点F,使△BFC的面积为6,如果存在,求出点F的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)2![]() ;(3)存在,理由见解析.
;(3)存在,理由见解析.
【解析】
(1)抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),则c=3,将点B的坐标代入抛物线表达式并解得:b=2,即可求解;
(2)函数的对称轴为:x=1,则点D(1,4),则BE=2,DE=4,即可求解;
(3)△BFC的面积=![]() ×BC×|yF|=2|yF|=6,解得:yF=±3,即可求解.
×BC×|yF|=2|yF|=6,解得:yF=±3,即可求解.
解:(1)抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),
则c=3,将点B的坐标代入抛物线表达式并解得:b=2,
故抛物线的表达式为:y=﹣x2+2x+3;
(2)函数的对称轴为:x=1,则点D(1,4),
则BE=2,DE=4,
BD=![]() =2
=2![]() ;
;
(3)存在,理由:
△BFC的面积=![]() ×BC×|yF|=2|yF|=6,
×BC×|yF|=2|yF|=6,
解得:yF=±3,
故:﹣x2+2x+3=±3,
解得:x=0或2或1![]() ,
,
故点F的坐标为:(0,3)或(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3);
,﹣3);


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C.
轴交于点C.
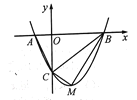
(1)请求出抛物线顶点M的坐标(用含k的代数式表示)以及A,B两点的坐标.
(2)试探究△BCM与△ABC的面积比值是否不变,若不变,试求出这个比值;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
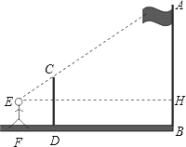
【题目】如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(CD)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(EF)1.6米,求旗杆的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
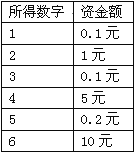
【题目】有时我们可以看到这样的转盘游戏:如图所示,你只要出1元钱就可以随意地转动转盘,转盘停止时指针落在哪个区域,你就按照这个区域所示的数字相应地顺时针跳过几格,然后按照下图所示的说明确定你的资金是多少.例如,当指针指向 “2”区域时候,你就向前跳过两个格到“5”,按奖金说明,“5”所示的资金为0.2元,你就可以得0.2元.请问这个游戏公平吗?能否用你所学的知识揭示其中的秘密?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种贺卡原售价每张1元,甲商店这种贺卡七折优惠,而在乙商店这种贺卡除了八折优惠外,购买30张以上(含30张)免费送5张. 设一次买这种贺卡x张(x是正整数且30≤x≤50),若选择在甲商店购买需用y1元,若选择在乙商店购买需用y2元.
(1)假定你代购买45张这种贺卡,请确定应在哪一个商店买花钱较少;
(2)请分别写出y1(元)与x(张)、y2(元)与x(张)之间的函数关系式;
(3)在x的取值范围内,试讨论在哪一个商店买花钱较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
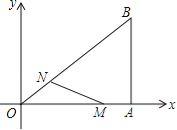
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
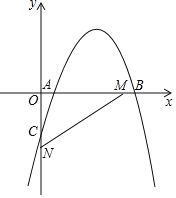
【题目】如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
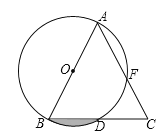
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于![]() 的方程
的方程![]() .
.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为![]() ,
,![]() (其中
(其中![]() ),若
),若![]() 是关于
是关于![]() 的函数,且
的函数,且![]() ,求这个函数的解析式;
,求这个函数的解析式;
(3)将(2)中所得的函数的图象在直线![]() 的左侧部分沿直线
的左侧部分沿直线![]() 翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当关于
翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当关于![]() 的函数
的函数![]() 的图象与此图象有两个公共点时,
的图象与此图象有两个公共点时,![]() 的取值范围是 (直接写出答案).
的取值范围是 (直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com