
【题目】某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图(如图).
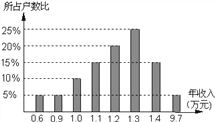
请你根据统计图给出的信息回答:
(1)这20个家庭的年平均收入为_____万元;
(2)样本中的中位数是_____万元,众数是_____万元;
(3)在平均数、中位数两数中,_____更能反映这个地区家庭的年收入水平.
【答案】 1.6, 1.2, 1.3, 中位数
【解析】分析:(1)根据加权平均数的计算公式分别进行计算即可;
(2)根据众数和中位数的定义分别进行解答即可;
(3)根据平均数,中位数两数的意义分别进行分析,即可得出答案.
详解:
(1)根据图示可知:平均收入为(20×0.05×0.6+20×0.05×0.9+20×0.1×1.0+20×0.15×1.1+20×0.2×1.2+20×0.25×1.3+20×0.15×1.4+20×0.05×9.7)÷20=32÷20=1.6(万元);
(2)因为共有20个数,数据中的第10和11个数据的平均数是中位数,所以中位数是1.2(万元);
因为众数是一组数据中出现次数最多的数,所以众数是1.3(万元);
(3)在平均数,中位数两数中平均数受到极端值的影响较大,所以中位数更能反映这个地区家庭的年收入水平.
故答案为:1.6,1.2,1.3,中位数.


科目:初中数学 来源: 题型:
【题目】在精准扶贫中,李师傅在当地政府的扶持下,去年下半年,他开办的桌椅加工厂取得了非常好的经济效益,他决定制作一批课桌捐赠给山区学校:已知制作一张桌子要用一个桌面和4条桌腿,1m3木材可制作20个桌面,或者制作400条桌腿,现有12m3木材,应怎样计划用料才能制作尽可能多的桌子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
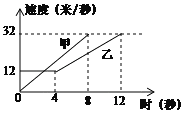
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
查看答案和解析>>
科目:初中数学 来源: 题型:
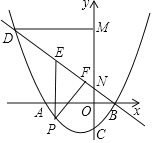
【题目】如图,抛物线![]() 与x轴交于A、B两点,其中点
与x轴交于A、B两点,其中点![]() ,交y轴于点
,交y轴于点![]() 直线
直线![]() 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点
过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点![]() 不与点B、D重合
不与点B、D重合![]() ,过点P作y轴的平行线,交直线BD于点E,过点D作
,过点P作y轴的平行线,交直线BD于点E,过点D作![]() 轴于点M.
轴于点M.
![]() 求抛物线
求抛物线![]() 的表达式及点D的坐标;
的表达式及点D的坐标;
![]() 若四边形PEMN是平行四边形?请求出点P的坐标;
若四边形PEMN是平行四边形?请求出点P的坐标;
![]() 过点P作
过点P作![]() 于点F,设
于点F,设![]() 的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点的左边,距离原点8个单位长度,点B在原点的右边.
(Ⅰ)求点A,点B对应的数;
(Ⅱ)数轴上点A以每秒1个单位长度出发向左移动,同时点B以每秒3个单位长度的速度向左移动,在点C处追上了点A,求点C对应的数.
(Ⅲ)已知在数轴上点M从点A出发向右运动,速度为每秒1个单位长度,同时点N从点B出发向右运动,速度为每秒2个单位长度,设线段NO的中点为P(O为原点),在运动的过程中,线段![]() 的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
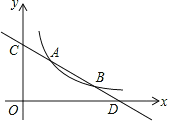
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com