
【题目】如图,矩形ABCD,点E, F分别在AD、BC上且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,若AB=![]() ,则CG为( )
,则CG为( )
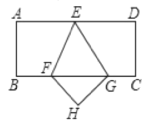
A.3.B.1.C.2.D.![]() .
.
【答案】B
【解析】
连接AF,根据矩形的性质、平行线的性质结合折叠的性质可得出∠AEF=∠AFE,即AF=AE,设BF=2x,则AD=BC=6x,AF=AE=FG=3x,CG=BC-BF-FG=x,在Rt△ABF中,利用勾股定理可求出x的值,此题得解.
连接AF,如图所示,
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
∴∠AEF=∠GFE.
由折叠的性质可知:AB=HG,BF=HF,∠ABF=∠GHF=90°,∠BFE=∠HFE,
∴△ABF≌△GHF,
∴AF=FG,∠AFB=∠GFH,
∴∠AFE=∠GFE,
∴∠AEF=∠AFE,
∴AF=AE.
设BF=2x,则AD=BC=6x,AF=AE=FG=3x,CG=BCBFFG=x.
在Rt△ABF中,∠B=90°,AB=![]() ,AF=3x,BF=2x,
,AF=3x,BF=2x,
∴AF2=AB2+BF2,即(3x)2=(2x)2+(![]() )2,
)2,
解得:x=1或x=1(舍去),
∴CG=x=1.
故选B.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
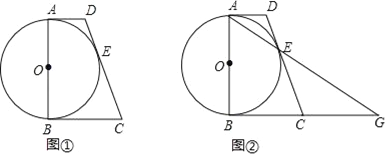
(1)求证:BC为⊙O的切线;
(2)连接AE并延长与BC的延长线交于点G(如图②所示).若AB=![]() ,CD=9,求线段BC和EG的长.
,CD=9,求线段BC和EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一元二次方程中,有著名的韦达定理:对于一元二次方程ax2+bx+c=0(a≠0),如果方程有两个实数根x1,x2,那么x1+x2=![]() ,x1+x2=
,x1+x2=![]() (说明:定理成立的条件△≥0).比如方程2x2-3x-1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=
(说明:定理成立的条件△≥0).比如方程2x2-3x-1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=![]() ,x1+x2=
,x1+x2=![]() .请阅读材料回答问题:
.请阅读材料回答问题:
(1)已知方程x2-3x-2=0的两根为x1、x2,求下列各式的值:
①x12+x22;②![]() ;
;
(2)已知x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根.
①是否存在实数k,使(2x1-x2)(x1-2x2)=![]() 成立?若存在,求出k的值;若不存在,请说明理由;
成立?若存在,求出k的值;若不存在,请说明理由;
②求使![]() -2的值为整数的实数k的整数值.
-2的值为整数的实数k的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家将于5月1日进行自驾游,由于交通便利,准备将行程分为上午和下午.上午的备选地点为:A—鼋头渚、B—常州淹城春秋乐园、C—苏州乐园,下午的备选地点为:D—常州恐龙园、E—无锡动物园.
(1)请用画树状图或列表的方法分析并写出小明家所有可能的游玩方式(用字母表示即可);
(2)求小明家恰好在同一城市游玩的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com