
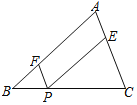
【题目】如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S△ABC=1.设BP=x,平行四边形AFPE的面积为y.
(1)求y与x的函数关系式;
(2)上述函数有最大值或最小值吗?若有,则当x取何值时,y有这样的值,并求出该值;若没有,请说明理由.
【答案】(1)y=-![]() x2+x;(2)当x=1时,y有最大值,最大值为
x2+x;(2)当x=1时,y有最大值,最大值为![]()
【解析】
(1)由平行四边形的性质得出PF∥CA,证出△BFP∽△BAC,得出面积比等于相似比的平方,得出S△BFP=![]() ,同理:S△PEC=(
,同理:S△PEC=(![]() )2,即可得出y与x的函数关系式;
)2,即可得出y与x的函数关系式;
(2)由![]() <0得出y有最大值,把(1)中函数关系式化成顶点式,即可得出结果.
<0得出y有最大值,把(1)中函数关系式化成顶点式,即可得出结果.
(1)∵四边形AFPE是平行四边形,
∴PF∥CA,∴△BFP∽△BAC,
∴![]() =(
=(![]() )2,
)2,
∵S△ABC=1,∴S△BFP=![]() ,
,
同理:S△PEC=(![]() )2=
)2=![]() ,
,
∴y=1-![]() -
-![]() ,
,
∴y=-![]() x2+x;
x2+x;
(2)上述函数有最大值,最大值为 ;理由如下:
∵y=-![]() x2+x =-
x2+x =-![]() (x﹣1)2+
(x﹣1)2+![]() ,又-
,又-![]() <0,
<0,
∴y有最大值,
∴当x=1时,y有最大值,最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
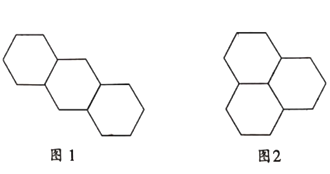
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是_______.有![]() 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则
个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
(1)求直线![]() 的表达式;
的表达式;
(2)过点A做平行于x轴的直线l,l与抛物线![]() (a>0)交于B,C两点。若BC≥4,求a的取值范围;
(a>0)交于B,C两点。若BC≥4,求a的取值范围;
(3)设直线![]() 与抛物线
与抛物线![]() 交于D,E两点,当3
交于D,E两点,当3![]() ≤DE≤5
≤DE≤5![]() 时,结合函数的图象,直接写出m的取值范围是____________________。
时,结合函数的图象,直接写出m的取值范围是____________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
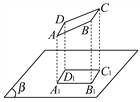
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
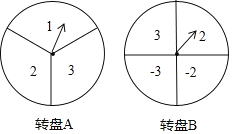
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别是A(﹣1,1),B(﹣4,1),C(﹣3,3).
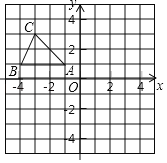
(1)将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;并判断以O,A1,B为顶点的三角形的形状(直接写出结果);
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2,并求出点C旋转到C2所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com