
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.

【答案】(1)y=﹣x2+4x;(2)线段OC的长度![]() ;(3)S△MOC最大值为
;(3)S△MOC最大值为![]() .
.
【解析】
(1)C1、C2:y=ax2+bx开口大小相同、方向相反,则a=-1,将点A的坐标代入C2的表达式,即可求解;
(2)点A关于C2对称轴的对称点是点O(0,0),连接OC交函数C2的对称轴与点P,此时PA+PC的值最小,即可求解;
(3)S△MOC=![]() MH×xC=
MH×xC=![]() (-x2+4x-x)= -
(-x2+4x-x)= -![]() x2+
x2+![]() x,即可求解.
x,即可求解.
(1)令:y=x2﹣2x=0,则x=0或2,即点B(2,0),
∵C1、C2:y=ax2+bx开口大小相同、方向相反,则a=﹣1,
则点A(4,0),将点A的坐标代入C2的表达式得:
0=﹣16+4b,解得:b=4,
故抛物线C2的解析式为:y=﹣x2+4x;
(2)联立C1、C2表达式并解得:x=0或3,
故点C(3,3),
连接OC交函数C2的对称轴与点P,
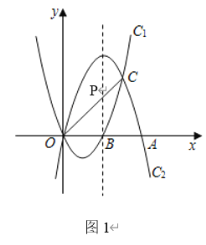
此时PA+PC的值最小为:线OC的长度![]() ;
;
设OC所在直线方程为:![]()
将点O(0,0),C(3,3)带入方程,解得k=1,
所以OC所在直线方程为:![]()
![]() 点P在函数C2的对称轴上,令x=2,带入直线方程得y=2,
点P在函数C2的对称轴上,令x=2,带入直线方程得y=2,
![]() 点P坐标为(2,2)
点P坐标为(2,2)
(3)由(2)知OC所在直线的表达式为:y=x,
过点M作y轴的平行线交OC于点H,
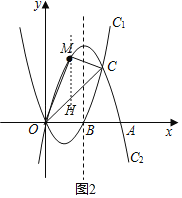
设点M(x,﹣x2+4x),则点H(x,x),则MH=﹣x2+4x﹣x
则S△MOC=S△MOH+S△MCH
=![]() MH×xC =
MH×xC = ![]() (﹣x2+4x﹣x)=
(﹣x2+4x﹣x)=![]()
∵△MOC的面积是一个关于x的二次函数,且开口向下
![]() 其顶点就是它的最大值。其对称轴为x=
其顶点就是它的最大值。其对称轴为x=![]() =
=![]() ,此时y=
,此时y=![]()
S△MOC最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】广宇、承义两名同学分别进行5次射击训练,训练成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
广宇 | 9 | 8 | 7 | 7 | 9 |
承义 | 6 | 8 | 10 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A.广宇训练成绩的平均数大于承义训练成绩平均数
B.广宇训练成绩的中位数与承义训练成绩中位数不同
C.广宇训练成绩的众数与承义训练成绩众数相同
D.广宇训练成绩比承义训练成绩更加稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设某商场地下停车场有5个出入口,每天早晨7点开始对外停车且此时车位空置率为90%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,6小时车库恰好停满;如果开放3个进口和2个出口,3小时车库恰好停满.2019年清明节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,因为车库改造,只能开放1个进口和1个出口,则从早晨7点开始经过______小时车库恰好停满.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
科目:初中数学 来源: 题型:
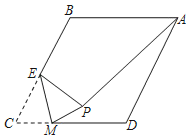
【题目】如图,在菱形ABCD中,点E是BC边的中点,动点M在CD边上运动,以EM为折痕将△CEM折叠得到△PEM,连接PA,若AB=4,∠BAD=60°,则PA的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
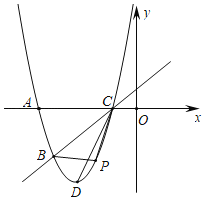
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=![]() (k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM=2MA,若AB=3,那么点N的横坐标为( )
(k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM=2MA,若AB=3,那么点N的横坐标为( )
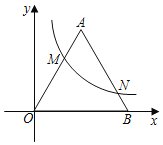
A.![]() B.
B.![]() C.4D.6
C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
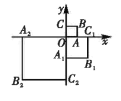
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的顶点
的顶点![]() 分别在
分别在![]() ,
,![]() 轴上,且
轴上,且![]() .将正方形
.将正方形![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() ,且
,且![]() ,得到正方形
,得到正方形![]() ,再将正方
,再将正方![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() ,且
,且![]() ,得到正方形
,得到正方形![]() ,以此规律,得到正方形
,以此规律,得到正方形![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com