
【题目】如图,已知一个抛物线经过A(0,1),B(1,3),C(﹣1,1)三点.
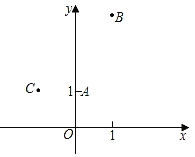
(1)求这个抛物线的表达式及其顶点D的坐标;
(2)联结AB、BC、CA,求tan∠ABC的值;
(3)如果点E在该抛物线的对称轴上,且以点A、B、C、E为顶点的四边形是梯形,直接写出点E的坐标.
【答案】(1)y=x2+x+1,顶点D的坐标(﹣![]() ,
,![]() );(2)tan∠ABC=
);(2)tan∠ABC=![]() ;(3)点E的坐标为(﹣
;(3)点E的坐标为(﹣![]() ,3)或(﹣
,3)或(﹣![]() ,2)或(﹣
,2)或(﹣![]() ,
,![]() )
)
【解析】
(1)设抛物线的解析式为y=ax2+bx+c,将A(0,1)、B(1,3)、C(﹣1,1)代入,求a、b、c的值,可得结果;
(2)如图,过点B作BF⊥x轴于F,延长CA交BF于点D,过点A作AM⊥BC于M,通过勾股定理和等腰直角三角形的性质可求AM和BM的长,即可求解;
(3)分三种情况讨论,由梯形的性质可求解.
解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0).
由题意可得:
解得:![]()
∴抛物线的解析式为:y=x2+x+1,
∵y=x2+x+1=![]() ,
,
∴顶点D的坐标(﹣![]() ,
,![]() );
);
(2)如图,过点B作BF⊥x轴于F,延长CA交BF于点D,过点A作AM⊥BC于M,
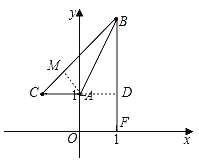
∴BF=3,
∵A(0,1),C(﹣1,1),
∴AC∥x轴,
∴CD⊥BF,
∴CD=BD=2,AD=1,CA=1,
∴BC=2![]() ,∠BCD=∠CBD=45°,
,∠BCD=∠CBD=45°,
∵AM⊥BC,
∴∠MAC=∠MCA=45°,
∴CM=AM,
∴CM=AM=![]() ,
,
∴BM=BC﹣CM=![]() ,
,
∴tan∠ABC=![]() =
=![]() ;
;
(3)∵A(0,1),B(1,3),C(﹣1,1),
∴直线AC解析式为:y=1,
直线AB解析式为:y=2x+1,
直线BC解析式为:y=x+2,
若BE∥AC,则点E的纵坐标为3,且点E在对称轴上,
∴点E(﹣![]() ,3);
,3);
若CE∥AB,则CE的解析式为;y=2x+3,
∵点E在对称轴上,
∴x=﹣![]() ,
,
∴y=2,
即点E(﹣![]() ,2);
,2);
若AE∥BC,则AE解析式为:y=x+1,
∵点E在对称轴上,
∴x=﹣![]() ,
,
∴y=![]() ,
,
即点E(﹣![]() ,
,![]() ),
),
综上所述:点E的坐标为(﹣![]() ,3)或(﹣
,3)或(﹣![]() ,2)或(﹣
,2)或(﹣![]() ,
,![]() ).
).


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】观察下列等式,探究其中的规律:①![]() +
+![]() ﹣1=
﹣1=![]() ,②
,②![]() +
+![]() ﹣
﹣![]() =
=![]() ,③
,③![]() +
+![]() ﹣
﹣![]() =
=![]() ,④
,④![]() +
+![]() ﹣
﹣![]() =
=![]() ,….
,….
(1)按以上规律写出第⑧个等式:_______;
(2)猜想并写出第n个等式:_________;
(3)请证明猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点M';③以点M'为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N';④过点N'作射线ON'交BC于点E.若AB=8,则线段OE的长为_______.
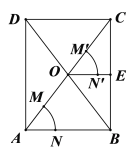
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y= ![]() +(1-2a)x(a>0),下列说法错误的是( )
+(1-2a)x(a>0),下列说法错误的是( )
A. 当![]() 时,该二次函数图象的对称轴为y轴
时,该二次函数图象的对称轴为y轴
B. 当a>![]() 时,该二次函数图象的对称轴在y轴的右侧
时,该二次函数图象的对称轴在y轴的右侧
C. 该二次函数的图象的对称轴可为x=1
D. 当x>2时,y的值随x的值增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的项点为
的项点为![]() ,交
,交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),且
点左侧),且![]() .
.
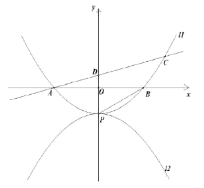
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)过点![]() 的直线交抛物线于点
的直线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 的面积被
的面积被![]() 轴分为1: 4两个部分,求直线
轴分为1: 4两个部分,求直线![]() 的解析式;
的解析式;
(3)在(2)的情况下,将抛物线![]() 绕点
绕点![]() 逆时针旋转180°得到抛物线
逆时针旋转180°得到抛物线![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,当点
上一点,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 为直角三角形?
为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于
内接于![]() ,
,![]() 是直径,点
是直径,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 交
交![]() 边于点
边于点![]() .
.
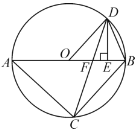
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() ,求四边形
,求四边形![]() 的面积(用含有
的面积(用含有![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
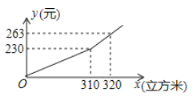
【题目】某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费,年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档,某户应交天然气费![]() (元)与年用天然气量
(元)与年用天然气量![]() (立方米)的关系如图所示,观察图像并回答问题:
(立方米)的关系如图所示,观察图像并回答问题:
(1)求![]() 与
与![]() 之间的函数解析式并写出自变量
之间的函数解析式并写出自变量![]() 的取值范围;
的取值范围;
(2)嘉琪家2018年天然气费为1029元,求嘉琪家2018年使用天然气量是否超出310立方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com