
 如图,在等腰梯形ABCD中,AD∥BC,AB=3,∠B=60°,DE∥AB,则CE等于
如图,在等腰梯形ABCD中,AD∥BC,AB=3,∠B=60°,DE∥AB,则CE等于 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
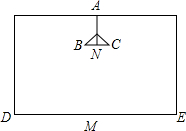 在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8m,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,
在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8m,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com