
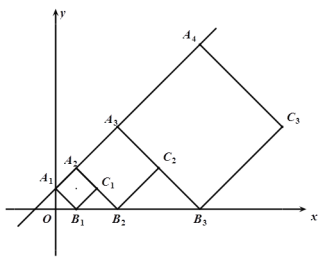
【题目】正方形![]() ,
, ![]() ,
,![]() ,…按如图所示的方式放置,点
,…按如图所示的方式放置,点![]() ,
,![]() ,
,![]() ,…和点
,…和点![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() (
(![]() )和
)和![]() 轴上。已知
轴上。已知![]() ,点
,点![]() ,则
,则![]() 的坐标是_____________
的坐标是_____________
【答案】![]()
【解析】
由题意可知A1纵坐标为1,A2的纵坐标为2,A3的纵坐标为4,A4的纵坐标为8,…,即可得到C1,C2,C3,C4,C5的纵坐标,根据图象得出C1(2,1),C2(5,2),C3(11,4),即可得到C1,C2,C3,C4,C5…在一条直线上,直线的解析式为y=![]() x+
x+![]() ,把C5的纵坐标代入即可求得横坐标.
,把C5的纵坐标代入即可求得横坐标.
解:由题意可知A1纵坐标为1,A2的纵坐标为2,A3的纵坐标为4,A4的纵坐标为8,…,
∵A1和C1,A2和C2,A3和C3,A4和C4的纵坐标相同,
∴C1,C2,C3,C4,C5的纵坐标分别为1,2,4,8,16,…
∴根据图象得出C1(2,1),C2(5,2),C3(11,4),
∴直线C1C2的解析式为y=![]() x+
x+![]() ,
,
∵A5的纵坐标为16,
∴C5的纵坐标为16,
把y=16代入y=![]() x+
x+![]() ,解得x=47,
,解得x=47,
∴C5的坐标是(47,16),
故答案为(47,16).


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .点
.点![]() 是平面内不与点
是平面内不与点![]() ,
,![]() 重合的任意一点.连接
重合的任意一点.连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
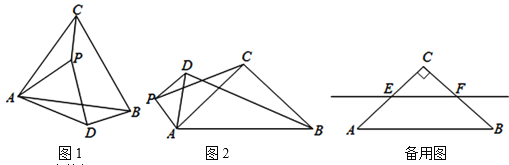
(1)观察猜想
如图1,当![]() 时,
时,![]() 的值是______,直线
的值是______,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是____________.(提示:求角度时可考虑延长
相交所成的较小角的度数是____________.(提示:求角度时可考虑延长![]() 交
交![]() 的延长线于
的延长线于![]() )
)
(2)类比探究
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的小角的度数,并就图2的情形说明理由.
相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当![]() 时,若点
时,若点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,请直接写出点
上,请直接写出点![]() ,
,![]() ,
,![]() 在同一直线上时
在同一直线上时![]() 的值_______________.
的值_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
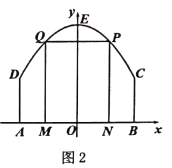
【题目】某景区平面图如图1所示,![]() 为边界上的点.已知边界
为边界上的点.已知边界![]() 是一段抛物线,其余边界均为线段,且
是一段抛物线,其余边界均为线段,且![]() ,抛物线顶点
,抛物线顶点![]() 到
到![]() 的距离
的距离![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
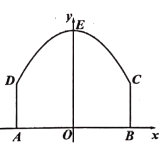
![]() 求边界
求边界![]() 所在抛物线的解析式;
所在抛物线的解析式;
![]() 如图2,该景区管理处欲在区域
如图2,该景区管理处欲在区域![]() 内围成一个矩形
内围成一个矩形![]() 场地,使得点
场地,使得点![]() 在边界
在边界![]() 上,点
上,点![]() 在边界
在边界![]() 上,试确定点
上,试确定点![]() 的位置,使得矩形
的位置,使得矩形![]() 的周长最大,并求出最大周长.
的周长最大,并求出最大周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中BC=2![]() ,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,
,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,![]() 的长为( )
的长为( )
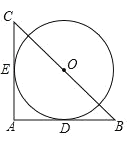
A.![]() B.
B.![]() C.πD.2π
C.πD.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
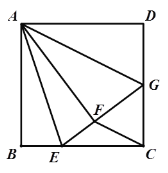
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() ,将正方形边
,将正方形边![]() 沿
沿![]() 折叠到
折叠到![]() ,延长
,延长![]() 交
交![]() 于
于![]() .连接
.连接![]() ,现在有如下四个结论:①
,现在有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ∥
∥![]() ;④
;④![]() ; 其中结论正确的个数是( )
; 其中结论正确的个数是( )
A.1B.2
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.
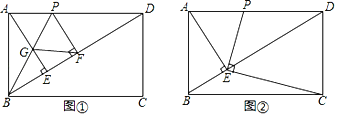
(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;
(2)若PE⊥EC,如图②,求证:AEAB=DEAP;
(3)在(2)的条件下,若AB=1,BC=2,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,是《算经十书》中最重要的一种,成于公元一世纪左右.在其“勾股”章中有这样一个问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD.EG=15里,HG经过点A,则FH等于多少里?请你根据上述题意,求出FH的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 与一次函数y2=ax+b的图象交于点A(﹣2,5)和点B(n,l).
与一次函数y2=ax+b的图象交于点A(﹣2,5)和点B(n,l).
(1)求反比例函数和一次函数的表达式;
(2)请结合图象直接写出当y1≥y2时自变量x的取值范围;
(3)点P是y轴上的一个动点,若S△APB=8,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com