考点:解一元一次方程
专题:
分析:(1)移项、合并同类项、系数化成1即可求解;
(2)移项、合并同类项、系数化成1即可求解;
(3)去括号、移项、合并同类项、系数化成1即可求解;
(4)去括号、移项、合并同类项、系数化成1即可求解;
(5)去括号、移项、合并同类项、系数化成1即可求解;
(6)去分母、去括号、移项、合并同类项、系数化成1即可求解;
(7)去分母、去括号、移项、合并同类项、系数化成1即可求解;
(8)去括号、移项、合并同类项、系数化成1即可求解.
解答:解:(1)移项,得:3x-x=11+5,
合并同类项,得:2x=16,
系数化成1得:x=8;
(2)移项,得:
=1,
系数化成1得:x=8;
(3)去括号,得:2x-2+10-5x=13,
移项,得:2x-5x=13+2-10,
合并同类项,得:-3x=5,
系数化成1得:x=-
;
(4)去括号,得:9x-3x+3=6,
移项,得:9x-3x=6-3,
合并同类项,得6x=3,
系数化成1得x=
;
(5)去分母,得:3(3y-1)-12=2(5y-7),
去括号,得9y-3-12=10y-14,
移项,得9y-10y=-14+3+12,
合并同类项,得-y=1,
系数化成1得y=-1;
(6)去分母,得3(x+2)-2(2x-3)=12,
去括号,得6x+6-4x+6=12,
移项,得6x-4x=12-6-6,
合并同类项,系数化成1得x=0;
(7)去分母,得:9(x-1)-6=5x-7,
去括号,得9x-9-6=5x-7,
移项,得9x-5x=-7+9+6,
合并同类项,得4x=8,
系数化成1得x=2;
(8)
x-(
x-
)=
x.
去括号,得
x-
x+
=
x,
移项,得
x-
x-
x=-
,
合并同类项,得-
x=-
,
系数化成1得x=3.
点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.



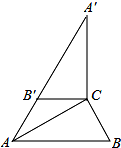 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )