
【题目】如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°.
(1)若AD=2,求AB;
(2)若AB+CD=2![]() +2,求AB.
+2,求AB.

【答案】(1)AB=![]() ;(2)AB=
;(2)AB=![]() +1.
+1.
【解析】试题分析:(1)根据∠A=∠C=45°,∠ADB=∠ABC=105°,得到∠BDF=∠ADC﹣∠ADB=165°﹣105°=60°,△ADE与△BCF为等腰直角三角形,即可求出AE的长,利用锐角三角函数可求得BE的长,从而得到AB的长;
(2)设DE=x,利用(1)的某些结论,特殊角的三角函数和勾股定理,表示AB,CD,即可得到答案.
(1)过A点作DE⊥AB,过点B作BF⊥CD,∵∠A=∠C=45°,∠ADB=∠ABC=105°,∴∠ADC=360°﹣∠A﹣∠C﹣∠ABC=360°﹣45°﹣45°﹣105°=165°,∴∠BDF=∠ADC﹣∠ADB=165°﹣105°=60°,△ADE与△BCF为等腰直角三角形,∵AD=2,∴AE=DE=![]() =
=![]() ,∵∠ABC=105°,∴∠ABD=105°﹣45°﹣30°=30°,∴BE=
,∵∠ABC=105°,∴∠ABD=105°﹣45°﹣30°=30°,∴BE=![]() =
=![]() =
=![]() ,∴AB=
,∴AB=![]() ;
;
(2)设DE=x,则AE=x,BE=![]() =
=![]() =
=![]() ,∴BD=
,∴BD=![]() =2x,∵∠BDF=60°,∴∠DBF=30°,∴DF=
=2x,∵∠BDF=60°,∴∠DBF=30°,∴DF=![]() BD=x,∴BF=
BD=x,∴BF=![]() =
=![]() =
=![]() ,∴CF=
,∴CF=![]() ,∵AB=AE+BE=
,∵AB=AE+BE=![]() ,CD=DF+CF=
,CD=DF+CF=![]() ,AB+CD=
,AB+CD=![]() ,∴AB=
,∴AB=![]() .
.



 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
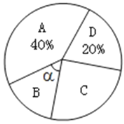
【题目】2019年10月,某市高质量通过全国文明城市测评,该成绩的取得得益于领导高度重视(A)、整改措施有效(B)、市民积极参与(C)、市民文明素质(D).某数学兴趣小组随机走访了部分市民,对这四项认可度进行调查(只选填最认可的一项),并将调查结果制作了如下两幅不完整的统计图.
(1)请补全D项的条形图;
(2)已知B、C两项条形图的高度之比为3:5.
①选B、C两项的人数各为多少个?
②求α的度数,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误结论有( );①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在![]() 中,若
中,若![]() ,则
,则![]() 为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com