
在一次数学课上,李老师出示一道题目:
| 如图,在△ABC中,AC=BC,AD=BD,∠A=30°,在线段AB上求作两点P,Q,使AP=CP=CQ=BQ. |
明明作法:分别作∠ACD和∠BCD的平分线,交AB于点P,Q.点P,Q就是所求作的点.
晓晓作法:分别作AC和BC的垂直平分线,交AB于点P,Q.点P,Q就是所求作的点.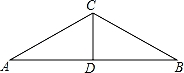
你认为明明和晓晓作法正确的是( )
A.明明 B.晓晓 C.两人都正确 D.两人都错误
C【考点】角平分线的性质;线段垂直平分线的性质.
【分析】根据等腰三角形的性质得到∠B=∠A=30°,CD⊥AB,由三角形的内角和得到∠ACD=∠BCD=60°,
明明作法:如图1,根据角平分线的定义得到∠ACP=∠BCQ=30°,求得∠A=∠ACP,∠B=∠BCQ,由等腰三角形的判定得到AP=PC,BQ=CQ,根据全等三角形的性质得到AP=BQ,于是得到AP=CP=CQ=BQ;故明明作法正确;
晓晓作法:如图2,根据线段垂直平分线的性质得到AP=PC,BQ=CQ,推出△APC≌△BCQ,根据全等三角形的性质得到AP=BQ,求得AP=CP=CQ=BQ,于是得到晓晓作法正确.
【解答】解:∵AC=BC,AD=BD,
∴∠B=∠A=30°,CD⊥AB,
∴∠AC D=∠BCD=60°,
D=∠BCD=60°,
明明作法:如图1,
∵CP平分∠ACD,CQ平分∠BCD,
∴∠ACP=∠BCQ=30°,
∴∠A=∠ACP,∠B=∠BCQ,
∴AP=PC,BQ=CQ,
在△ACP与△BCQ中,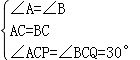 ,
,
∴△APC≌△BCQ,
∴AP=BQ,
∴AP=CP=CQ=BQ;
∴明明作法正确;
晓晓作法:如图2,
∵分别作AC和BC的垂直平分线,交AB于点P,Q,
∴AP=PC,BQ=CQ,在△ACP与△BCQ中,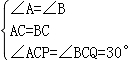 ,
,
∴△APC≌△BCQ,
∴AP=BQ,
∴AP=CP=CQ=BQ,
∴晓晓作法正确,
故选C.
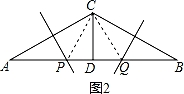

【点评】本题考查了角平分线的性质,线段垂直平分线的性质,全等三角形的判定和性质,等腰三角形的性质,正确的画出图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
双十一”当天,某淘宝网店做出优惠活动,按原价应付额不超过200元的一律9折优惠,超过200元的,其中200元按9折算,超过200元的部分按8折算.设某买家在该店购物按原价应付x元,优惠后实付y元.
(1)当x>200时,试写出y与x之间的函数关系式(如果是一次函数,请写成y=kx+b的形式);
(2)该买家挑选的商品按原价应付300元,求优惠后实付多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )
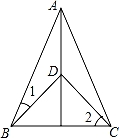
A.大40° B.小40° C.大30° D.小30°
查看答案和解析>>
科目:初中数学 来源: 题型:
作图与证明:
(1)读下列语句,作出符合题意的图形(要求:使用直尺和圆规作图,保留作图痕迹).
①作线段AB;
②分别以A,B为圆心,以AB长为半径作弧,两弧在线段AB的同侧交于点C;
③连接AC,以点C为圆心,以AB长为半径作弧,交AC延长线于点D;
④连接BD,得△ABD.
(2)求证:△ABD是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
为了市民出行更加方便,天津市政府大力发展公共交通,2013年天津市公共交通客运量约为1608000000人次,将1608000000用科学记数法表示为( )
A.160.8×107 B.16.08×108 C.1.608×109 D.0.1608×1010
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com