
【题目】如图1,已知抛物线;C1:y=﹣![]() (x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
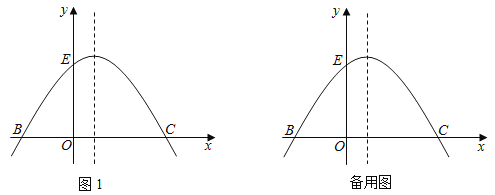
(1)求点B、点C的坐标;
(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;
(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
【答案】(1)点B、C的坐标分别为:(﹣2,0)、(m,0);(2)存在,点H(1,![]() b);(3)存在,m=2
b);(3)存在,m=2![]()
【解析】
(1)![]() ,令y=0,则x=﹣2或m,即可求解;
,令y=0,则x=﹣2或m,即可求解;
(2)点B关于函数对称轴的对称点为点C(m,0),连接CE交对称轴于点H,则点H为所求,即可求解;
(3)分△BEC∽△BCF、△BEC∽△FCB两种情况,分别求解即可.
解:(1)![]() ,令y=0,则x=﹣2或m,
,令y=0,则x=﹣2或m,
故点B、C的坐标分别为:(﹣2,0)、(m,0);
(2)存在,理由:
![]() ,令x=0,则y=2,故点E(0,2),
,令x=0,则y=2,故点E(0,2),
△BCE的面积为:![]() ,解得:m=4,
,解得:m=4,
则抛物线的对称轴为: ![]() ,
,
点B关于函数对称轴的对称点为点C(m,0),连接CE交对称轴于点H,则点H为所求,
将点C、E的坐标代入一次函数表达式并解得:
直线CE的表达式为: ![]() ,当x=1时,
,当x=1时,![]() ,
,
故点H(1,![]() b);
b);
(3)∵OE=OB=2,故∠EBO=45°,

过点F作FT⊥x轴于点F;
①当△BEC∽△BCF时,
则BC2=BEBF,∠FBO=EBO=45°,
则直线BF的函数表达式为:y=﹣x﹣2,故点F(x,﹣x﹣2);
将点F的坐标代入抛物线表达式得: ![]()
解得:x=﹣2(舍去)或2m,
故点F(2m,﹣2m﹣2),
则![]()
∵BC2=BEBF,
则![]() 解得:
解得: ![]() (舍去负值),
(舍去负值),
故![]()
②当△BEC∽△FCB时,
则BC2=BFEC,∠CBF=∠ECO,
则△BFT∽△COE,
则![]() ,则点
,则点![]()
将点F的坐标代入抛物线表达式得: ![]()
解得:x=﹣2(舍去)或m+2;
则点![]()
BC2=BFEC,则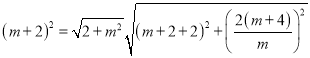
化简得:m3+4m2+4m=m3+4m2+4m+16,
此方程无解;
综上,m=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
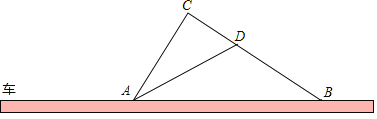
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2020年中考,某中学对全校九年级学生进行了一次数学期末模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题:
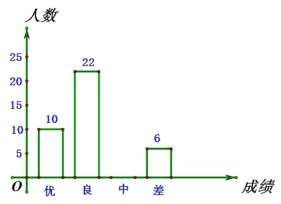
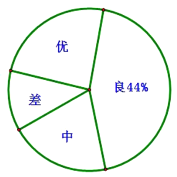
(1)在这次调查中,一共调查了多少名学生;
(2)将条形统计图补充完整;
(3)若该中学九年级共有860人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,按以下步骤作图:①以点A为圆心,AB的长为半径作弧,交AD于点F;②分别以点F,B为圆心大于![]() FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )
FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )

A.12B.20C.24D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点坐标为(1,2),那么下列结论中:①abc>0;②2a+b═0;③b2﹣4ac>0;④若关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,则m>2;⑤方程|ax2+bx+c|=1有四个根,则这四个根的和为4.正确的个数为( )
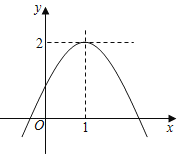
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,探究函数图象和性质过程如下:
,探究函数图象和性质过程如下:
(1)下表是y与x的几组值,则解析式中的m= ,表格中的n= ;
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y |
|
|
| 1 |
| 3 |
| 4 |
| 3 | n | 0 | … |
(2)在平面直角坐标系中描出表格中各点,并画出函数图象:
(3)若A(x1,y1)、B(x2,y2)、C(x3,y3)为函数图象上的三个点,其中x2+x3>4且﹣1<x1<0<x2<2<x3<4,则y1、y2、y3之间的大小关系是 ;
(4)若直线y=k+1与该函数图象有且仅有一个交点,则k的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
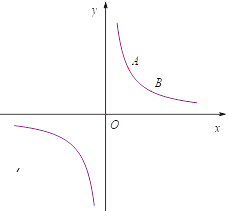
【题目】如图所示,已知![]() 点的横坐标为2,将
点的横坐标为2,将![]() 点向右平移2个单位,再向下平移2个单位得到
点向右平移2个单位,再向下平移2个单位得到![]() 点,且
点,且![]() 、
、![]() 两点均在双曲线
两点均在双曲线![]() 上.
上.
(1)求反比例函数的解析式.(2)若直线![]() 于反比例函数
于反比例函数![]() 的另一交点为
的另一交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
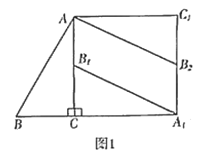
![]() 操作发现:如图1,在
操作发现:如图1,在![]() 中,
中,![]() ,以点
,以点![]() 为中心,把
为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ;再以点
;再以点![]() 为中心,把
为中心,把![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() .连接
.连接![]() .则
.则![]() 与
与![]() 的位置关系为平行;
的位置关系为平行;
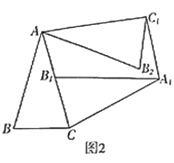
![]() 探究证明:如图2,当
探究证明:如图2,当![]() 是锐角三角形,
是锐角三角形,![]() 时,将
时,将![]() 按照(1)中的方式,以点
按照(1)中的方式,以点![]() 为中心,把
为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ;再以点
;再以点![]() 为中心,把
为中心,把![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() .连接
.连接![]() ,
,
①探究![]() 与
与![]() 的位置关系,写出你的探究结论,并加以证明;
的位置关系,写出你的探究结论,并加以证明;
②探究![]() 与
与![]() 的位置关系,写出你的探究结论,并加以证明.
的位置关系,写出你的探究结论,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.

(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com