
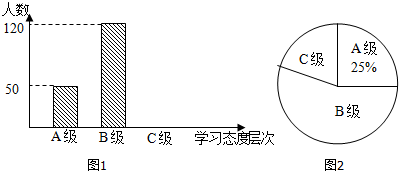
���� ��1������A������������ռ�İٷֱ���ʽ���м��㼴������������ѧ���������ٸ������������C�������������������ͼ2��C�����ε�Բ�Ľǣ�Ȼ��ȫ����ͳ��ͼ���ɣ�
��2����4�����¼���ѧ����������2��������2��Ů���ֱ�Ϊ1��2��3��4��B������3����������ѧ����������2��������1��Ů���ֱ�Ϊ0��1��3�������оٷ�������⣮
��� �⣺��1�������ѧ������Ϊ��$\frac{50}{25%}$=200����
����C��ѧ������Ϊ��200-50-120=30����
��C�����ε�Բ�Ľ�=360���$\frac{30}{200}$��100%=54��
�ʴ�Ϊ��200��54��
��ȫͳ��ͼ��ͼ��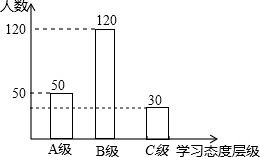
��2���б����£���4�����¼���ѧ����������2��������2��Ů���ֱ�Ϊ1��2��3��4��B������3����������ѧ����������2��������1��Ů���ֱ�Ϊ0��1��3��
| 1 | 2 | 3 | 4 | |
| 0 | 1��0 | 2��0 | 3��0 | 4��0 |
| 1 | 1��1 | 2��1 | 3��1 | 4��1 |
| 3 | 3��1 | 3��2 | 3��3 | 4��3 |
���� ���⿼���������ͳ��ͼ������ͳ��ͼ���ۺ������Լ�������¼��ĸ��ʣ�����ͳ��ͼ���Ӳ�ͬ��ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼ������ر�ʾ��ÿ����Ŀ�����ݣ�����ͳ��ͼֱ�ӷ�ӳ����ռ����İٷֱȴ�С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=ax2+bx+1�����㣨2��6��������ֱ��y=$\frac{1}{2}$x+1�ཻ��A��B���㣬��A��y���ϣ�����B��BC��x�ᣬ����Ϊ��C��4��0����
��ͼ��������y=ax2+bx+1�����㣨2��6��������ֱ��y=$\frac{1}{2}$x+1�ཻ��A��B���㣬��A��y���ϣ�����B��BC��x�ᣬ����Ϊ��C��4��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
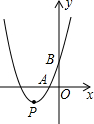 ��ͼ��������y=x2+bx+3����ΪP���ҷֱ���x�ᡢy�ύ��A��B���㣬��A�ڵ�P���Ҳ࣬tan��ABO=$\frac{1}{3}$��
��ͼ��������y=x2+bx+3����ΪP���ҷֱ���x�ᡢy�ύ��A��B���㣬��A�ڵ�P���Ҳ࣬tan��ABO=$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
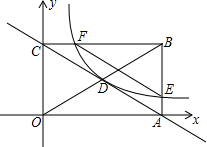 ��ͼ��ֱ��$y=-\frac{2}{m}x+4��mΪ������$�������ύ��A��C���㣬˫����$y=\frac{k}{x}��x��0��$��������OABC�Խ��ߵĽ���D����AB�߽��ڵ�E����BC���ڵ�F������BEF�����Ϊ9����k=��������
��ͼ��ֱ��$y=-\frac{2}{m}x+4��mΪ������$�������ύ��A��C���㣬˫����$y=\frac{k}{x}��x��0��$��������OABC�Խ��ߵĽ���D����AB�߽��ڵ�E����BC���ڵ�F������BEF�����Ϊ9����k=��������| A�� | 4 | B�� | 6 | C�� | 8 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڳ�����ABCD�У�CD��BC�ij��ȱ�Ϊ5��12�����ó����ε��ܳ�Ϊ34����BD�ij�Ϊ��������
��ͼ���ڳ�����ABCD�У�CD��BC�ij��ȱ�Ϊ5��12�����ó����ε��ܳ�Ϊ34����BD�ij�Ϊ��������| A�� | 13 | B�� | 12 | C�� | 8 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��1=��2��AC=AD������һ��������ʹ��ABC�ա�AEDAB=AE��
��ͼ����֪��1=��2��AC=AD������һ��������ʹ��ABC�ա�AEDAB=AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��� | B�� | ƽ�� | ||
| C�� | �����ƽ�� | D�� | �����ƽ�л��������ͬһֱ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com