
【题目】某商场购进了一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元为了尽快减少库存,商场决定采取适当的降价措施.调查发现,如果这种衬衫的售价每降低
元为了尽快减少库存,商场决定采取适当的降价措施.调查发现,如果这种衬衫的售价每降低![]() 元,那么该商场平均每天可多售出
元,那么该商场平均每天可多售出![]() 件.
件.
(1)若该商场计划平均每天盈利![]() 元,则每件衬衫应降价多少元?
元,则每件衬衫应降价多少元?
(2)该商场平均每天盈利能否达到![]() 元?
元?
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长均为 1.格点三角形 ABC(顶点是网格线交点的三角形)的顶点 A、C 的坐标分别是(﹣2,0),(﹣3,3).
(1)请在图中的网格平面内建立平面直角坐标系,写出点 B 的坐标;
(2)把△ABC 绕坐标原点 O 顺时针旋转 90°得到△A1B1C1,画出△A1B1C1,写出点
B1的坐标;
(3)以坐标原点 O 为位似中心,相似比为 2,把△A1B1C1 放大为原来的 2 倍,得到△A2B2C2 画出△A2B2C2,使它与△AB1C1 在位似中心的同侧;
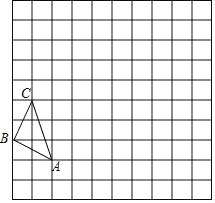
请在 x 轴上求作一点 P,使△PBB1 的周长最小,并写出点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为两把按不同比例尺进行刻度的直尺,每把直尺的刻度都是均匀的,已知两把直尺在刻度10处是对齐的,且上面的直尺在刻度15处与下面的直尺在刻度18处也刚好对齐,则上面直尺的刻度16与下面直尺对应的刻度是( )
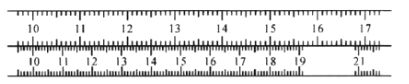
A.19.4B.19.5C.19.6D.19.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正三角形ABC的边长AB是480毫米.一质点D从点B出发,沿BA方向,以每秒钟10毫米的速度向点A运动.
(1)建立合适的直角坐标系,用运动时间t(秒)表示点D的坐标;
(2)过点D在三角形ABC的内部作一个矩形DEFG,其中EF在BC边上,G在AC边上.在图中找出点D,使矩形DEFG是正方形(要求所表达的方式能体现出找点D的过程);
(3)过点D、B、C作平行四边形,当t为何值时,由点C、B、D、F组成的平行四边形的面积等于三角形ADC的面积,并求此时点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像与双曲线
的图像与双曲线![]()
![]() 相交于
相交于![]() 和
和![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .
.
(1)求一次函数的解析式;
(2)根据图像直接写出不等式![]() 的解集;
的解集;
(3)![]() 的面积为
的面积为
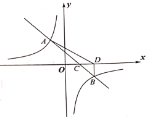
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )
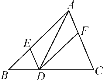
A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
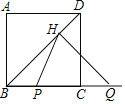
【题目】如图,正方形ABCD的边长为2,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )
A.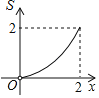 B.
B.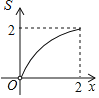
C.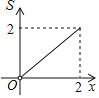 D.
D.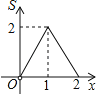
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax﹣3a(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
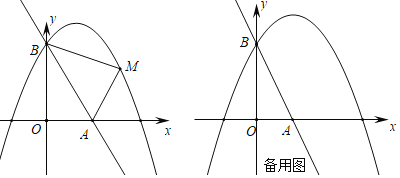
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图11①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图10②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73)
=1.73)
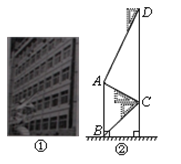
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com