
分析 (1)归纳总结得到一般性规律,写出第n项,表示出变形结果即可;
(2)原式利用得出的规律变形,计算即可得到结果;
(3)原式利用得出的规律变形,计算即可得到结果.
解答 解:(1)第n项为$\frac{1}{n(n+1)}$,可表示为$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…=$\frac{1}{2009}$-$\frac{1}{2010}$=1-$\frac{1}{2010}$=$\frac{2009}{2010}$;
(3)原式=$\frac{1}{2}$[$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2n}$-$\frac{1}{2(n+1)}$]=$\frac{n}{4(n+1)}$.
故答案为:(1)$\frac{1}{n(n+1)}$,$\frac{1}{n}$-$\frac{1}{n+1}$;(2)$\frac{2009}{2010}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:填空题
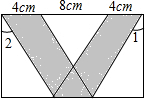 如图,在一个矩形中,有一个“V”字型的阴影图形,两个平行四边形交叉放在一起,∠1=∠2=30°,则阴影部分的面积S=44$\sqrt{3}$cm2.
如图,在一个矩形中,有一个“V”字型的阴影图形,两个平行四边形交叉放在一起,∠1=∠2=30°,则阴影部分的面积S=44$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
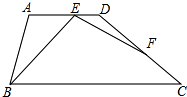 如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点F在DC上,且∠BEF=∠A.
如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点F在DC上,且∠BEF=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com