
分析 (1)根据上述材料给出的方法计算其相应的价值即可;
(2)按照三个数不同的顺序排列算出价值,由计算可以看出,要求得这些数列的价值的最小值;只有当前两个数的和的绝对值最小,最小只能为|-3+2|=1,由此得出答案即可;
(3)分情况算出对应的数值,建立方程求得a的数值即可.
解答 解:(1)因为|-4|=4,|$\frac{-4-3}{2}$|=3.5,|$\frac{-4-3+2}{3}$|=$\frac{5}{3}$,
所以数列-4,-3,2的价值为$\frac{5}{3}$,
故答案为:$\frac{5}{3}$;
(2)数列的价值的最小值为|$\frac{-3+2}{2}$|=$\frac{1}{2}$,
数列可以为:-3,2,-4,或2,-3,-4,
故答案为:$\frac{1}{2}$;-3,2,-4,或2,-3,-4;
(3)当|$\frac{2+a}{2}$|=1,则a=0,不合题意;
当|$\frac{-9+a}{2}$|=1,则a=11;
当|$\frac{2-9+a}{3}$|=1,则a=4.
故答案为:11或4.
点评 此题考查了算术平均数的定义以及数字的变化规律,理解运算的方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
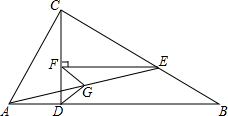 己知:如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,E是CB上一点,且CE=AC,EF⊥CD,垂足为F.
己知:如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,E是CB上一点,且CE=AC,EF⊥CD,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
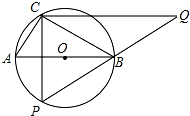 如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.
如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com