
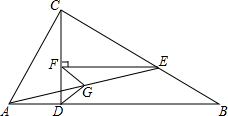
 己知:如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,E是CB上一点,且CE=AC,EF⊥CD,垂足为F.
己知:如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,E是CB上一点,且CE=AC,EF⊥CD,垂足为F.分析 (1)利用已知条件证明Rt△ADC≌Rt△CFE,根据全等三角形的对应边相等即可解答;
(2)连接CG,得到△ACE为等腰直角三角形,根据等腰直角三角形的性质得到CG⊥AE,∠CAG=∠ECG=45°,CG=AG=GE,再证明△GAD≌△GCF,得到∠AGD=∠CGF,根据CG⊥AE,得到∠AGF+∠CGF=90°,利用等量代换即可解答.
解答 解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠ECF=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠ECF,
在Rt△ADC和Rt△CFE中,
$\left\{\begin{array}{l}{∠CAD=∠ECF}\\{∠ADC=∠CFE=90°}\\{AC=CE}\end{array}\right.$
∴Rt△ADC≌Rt△CFE,
∴AD=CF.
(2)如图,连接CG,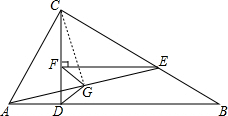
∵∠ACB=90°,G为AE的中点,AC=CE,
∴CG⊥AE,∠CAG=∠ECG=45°,CG=AG=GE,
∵Rt△ADC≌Rt△CFE,
∴∠CAD=∠ECF,
∵∠CAG+∠GAD=∠CAD,∠ECG+∠GCF=∠ECF,
∴∠GAD=∠GCF,
在△GAD和△GCF中,
$\left\{\begin{array}{l}{AG=CG}\\{∠GAD=∠GCF}\\{AD=CF}\end{array}\right.$
∴△GAD≌△GCF,
∴∠AGD=∠CGF,
∵CG⊥AE,
∴∠AGC=90°,
∴∠AGF+∠CGF=90°,
∴∠AGF+∠AGD=90°,
即∠DGF=90°,
∴GD⊥GF.
点评 本题考查了全等三角形的性质定理和判定定理,解决本题的关键是证明三角形全等.


科目:初中数学 来源: 题型:填空题
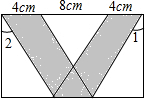 如图,在一个矩形中,有一个“V”字型的阴影图形,两个平行四边形交叉放在一起,∠1=∠2=30°,则阴影部分的面积S=44$\sqrt{3}$cm2.
如图,在一个矩形中,有一个“V”字型的阴影图形,两个平行四边形交叉放在一起,∠1=∠2=30°,则阴影部分的面积S=44$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
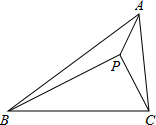 如图,△ABC中,∠BAC=60°,AB=2AC,点P在△ABC内,且PA=$\sqrt{3}$,PB=5,PC=2,则△ABC的面积为( )
如图,△ABC中,∠BAC=60°,AB=2AC,点P在△ABC内,且PA=$\sqrt{3}$,PB=5,PC=2,则△ABC的面积为( )| A. | 3+$\frac{7}{2}$$\sqrt{3}$ | B. | 3+$\frac{5}{2}$$\sqrt{3}$ | C. | 3+$\sqrt{3}$ | D. | 3+$\frac{1}{2}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
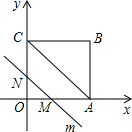 在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动.设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,则S与t之间函数关系式为S=$\left\{\begin{array}{l}{\frac{3}{8}{t}^{2}(0<t≤4)}\\{-\frac{3}{8}{t}^{2}+3t(4<t<8)}\end{array}\right.$.(结果化到最简)
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动.设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,则S与t之间函数关系式为S=$\left\{\begin{array}{l}{\frac{3}{8}{t}^{2}(0<t≤4)}\\{-\frac{3}{8}{t}^{2}+3t(4<t<8)}\end{array}\right.$.(结果化到最简)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com