
分析 先在平面直角坐标系中描出各点,再找出四条线段的中点坐标吗,然后比较中点的横坐标与纵坐标分别与对应线段的两个端点的横坐标和纵坐标可得:线段中点的横坐标为线段两端点的横坐标的平均数,线段中点的纵坐标为线段两端点的纵坐标的平均数.
解答 解: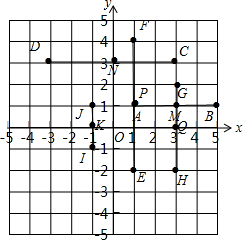 如图,线段AB的中点M的坐标为(3,1);线段CD的中点N的坐标为(0,3);线段EF的中点P的坐标为(1,1);
如图,线段AB的中点M的坐标为(3,1);线段CD的中点N的坐标为(0,3);线段EF的中点P的坐标为(1,1);
线段GH的中点Q的坐标为(3,0);线段IJ的中点K的坐标为(-1,0),
由上述中点的横坐标与纵坐标分别与对应线段的两个端点的横坐标和纵坐标进行比较得到,线段中点的横坐标为线段两端点的横坐标的平均数,线段中点的纵坐标为线段两端点的纵坐标的平均数.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;记住特殊位置点的坐标特征.


科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为$\frac{\sqrt{3}}{2}$.
如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
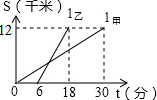 甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走$\frac{3}{5}$千米.
甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走$\frac{3}{5}$千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
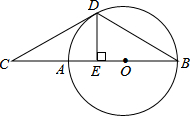 如图,△BCD中,DE⊥BC于点E,点O为BE上一点,以点O为圆心,OB为半径的圆经过点D,交BC于点A,已知∠CDE=2∠B
如图,△BCD中,DE⊥BC于点E,点O为BE上一点,以点O为圆心,OB为半径的圆经过点D,交BC于点A,已知∠CDE=2∠B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
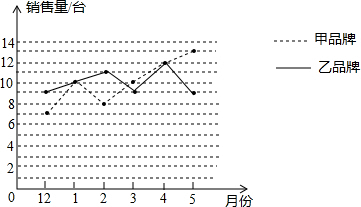
| 平均数 | 方差 | |
| 甲品牌销售量/台 | 10 | $\frac{13}{3}$ |
| 乙品牌销售量/台 | 10 | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
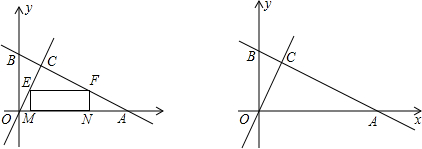
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com