
【题目】已知抛物线![]() (
(![]() 是常数)的顶点为
是常数)的顶点为![]() ,直线
,直线![]()

![]() 求证:点
求证:点![]() 在直线
在直线![]() 上;
上;
![]() 当
当![]() 时,抛物线与
时,抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 是
是![]() 轴下方抛物线上的一点,
轴下方抛物线上的一点,![]() (如图),求点
(如图),求点![]() 的坐标;
的坐标;
![]() 若以抛物线和直线
若以抛物线和直线![]() 的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的
的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的![]() 的值.
的值.
【答案】(1)证明见解析;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() 的值为
的值为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)利用配方法得到![]() ,点
,点![]() ,然后根据一次函数图象上点的坐标特征判断点
,然后根据一次函数图象上点的坐标特征判断点![]() 在直线
在直线![]() 上;
上;
(2)当![]() 时,抛物线解析式为
时,抛物线解析式为![]() ,根据抛物线与
,根据抛物线与![]() 轴的交点问题求出
轴的交点问题求出![]() ,易得
,易得![]() ,通过解方程组
,通过解方程组![]() ,得
,得![]() ,
,![]() ,作
,作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,如图,证明
,如图,证明![]() ,利用相似得
,利用相似得![]() ,设
,设![]() ,则
,则![]() ,得
,得![]() (舍去),
(舍去),![]() ,于是得到点
,于是得到点![]() 的坐标为
的坐标为![]() ;
;
(3)通过解方程组![]() 得
得![]() ,
,![]() ,利用两点间的距离公式得到
,利用两点间的距离公式得到![]() ,
,![]() ,然后分类讨论:当
,然后分类讨论:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,再分别解关于
,再分别解关于![]() 的方程求出
的方程求出![]() 即可.
即可.
![]() 证明:∵
证明:∵![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵当![]() 时,
时,![]() ,
,
∴点![]() 在直线
在直线![]() 上;
上;
![]() 解:当
解:当![]() 时,抛物线解析式为
时,抛物线解析式为![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
可得解方程组![]() ,解得
,解得![]() 或
或![]() ,
,
则![]() ,
,![]() ,
,
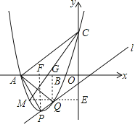
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,如图,
,如图,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
整理得![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
![]() 解:解方程组
解:解方程组![]() 得
得![]() 或
或![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
综上所述,![]() 的值为
的值为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
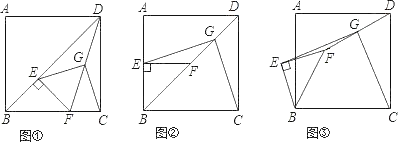
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)请问EG与CG存在怎样的数量关系,并证明你的结论;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有一块长方形活动场地,长为![]() 米,宽比长少
米,宽比长少![]() 米,实施“阳光体育”行动以后,学校为了扩大学生的活动场地,让学生能更好地进行体育活动,将操场的长和宽都增加
米,实施“阳光体育”行动以后,学校为了扩大学生的活动场地,让学生能更好地进行体育活动,将操场的长和宽都增加![]() 米.
米.
(1)求活动场地原来的面积是多少平方米.(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,求活动场地面积增加后比原来多多少平方米.
,求活动场地面积增加后比原来多多少平方米.

查看答案和解析>>
科目:初中数学 来源: 题型:
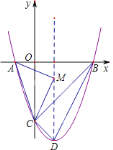
【题目】如图所示:抛物线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 、
、![]() 三点,
三点,![]() 是抛物线的顶点,
是抛物线的顶点,![]() 在对称轴上,
在对称轴上,![]() 在坐标轴上.以下结论:
在坐标轴上.以下结论:
①存在点![]() ,使
,使![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() 的最小值是
的最小值是![]() ;③
;③![]() 的最大值是
的最大值是![]() ;④若
;④若![]() 与
与![]() 相似,则
相似,则![]() 的坐标恰有两个.
的坐标恰有两个.
其中正确的是________(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
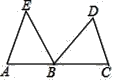
【题目】如图,在△ABE中,C为边AB延长线上一点,BC=AE,点D在∠EBC内部,且∠EBD=∠A=∠DCB.
(1)求证:△ABE≌△CDB.
(2)连结DE,若∠CDB=60°,∠AEB=50°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
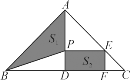
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=16 cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以![]() cm/s的速度向点D运动,过P点作矩形PDFE(E点在AC上),设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8).
cm/s的速度向点D运动,过P点作矩形PDFE(E点在AC上),设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8).
(1)经过几秒钟后,S1=S2?
(2)经过几秒钟后,S1+S2最大?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com