
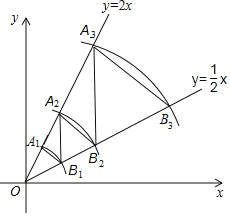
【题目】如图,在平面直角坐标系中,点A1的坐标为(1,2),以点O为圆心,以OA1长为半径画弧,交直线y=![]() x于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2,以O为圆心,以OA2长为半径画弧,交直线y=
x于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2,以O为圆心,以OA2长为半径画弧,交直线y=![]() x于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3,以点O为圆心,以OA3长为半径画弧,交直线y=
x于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3,以点O为圆心,以OA3长为半径画弧,交直线y=![]() x于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4,以点O为圆心,以OA4长为半径画弧,交直线y=
x于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4,以点O为圆心,以OA4长为半径画弧,交直线y=![]() x于点B4,…按照如此规律进行下去,点B2019的坐标为_____.
x于点B4,…按照如此规律进行下去,点B2019的坐标为_____.
科目:初中数学 来源: 题型:
【题目】在“弘扬传统文化,打造书香校园”的活动中,学校计划开展四项活动:“A﹣国学诵读”,“B﹣演讲”,“C﹣课本剧”,“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如图:
(1)如图,则被调查的总人数为 人;扇形统计图中,希望参加活动A所占圆心角为 度.
(2)根据题中信息补全条形统计图;
(3)学校现有1000名学生,请根据图中信息,估算全校学生希望参加活动D有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
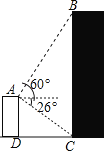
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:![]() ≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
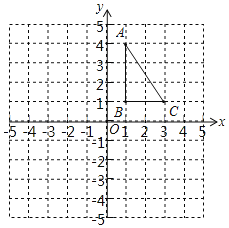
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC绕O点顺时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求点C划过的路径长度(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
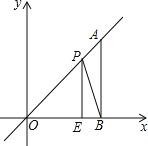
【题目】如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
A.4+2![]() B.4+
B.4+![]() C.6D.4
C.6D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是__________;位置关系是__________.
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)某种电子产品共![]() 件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品 件;
(2)如果从中任意取出![]() 件,利用列表或树状图求取出
件,利用列表或树状图求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
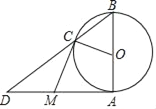
【题目】如图,AB是⊙O的直径,且AB=6,点M为⊙O外一点,且MA,MC分别切⊙O于点A、C.点D是两条线段BC与AM延长线的交点.
(1)求证:DM=AM;
(2)直接回答:
①当CM为何值时,四边形AOCM是正方形?
②当CM为何值时,△CDM为等边三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com