
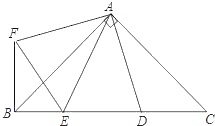
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,∠EAD=45°,将△ADC绕点A顺时针旋转90°,得到△AFB,连接EF.
(1)求证:EF=ED;
(2)若AB=2![]() ,CD=1,求FE的长.
,CD=1,求FE的长.
【答案】(1)见解析;(2)EF=![]() .
.
【解析】
(1)由旋转的性质可求∠FAE=∠DAE=45°,即可证△AEF≌△AED,可得EF=ED;
(2)由旋转的性质可证∠FBE=90°,利用勾股定理和方程的思想可求EF的长.
(1)∵∠BAC=90°,∠EAD=45°,
∴∠BAE+∠DAC=45°,
∵将△ADC绕点A顺时针旋转90°,得到△AFB,
∴∠BAF=∠DAC,AF=AD,CD=BF,∠ABF=∠ACD=45°,
∴∠BAF+∠BAE=45°=∠FAE,
∴∠FAE=∠DAE,AD=AF,AE=AE,
∴△AEF≌△AED(SAS),
∴DE=EF
(2)∵AB=AC=2![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=4,
∵CD=1,
∴BF=1,BD=3,即BE+DE=3,
∵∠ABF=∠ABC=45°,
∴∠EBF=90°,
∴BF2+BE2=EF2,
∴1+(3﹣EF)2=EF2,
∴EF=![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() 的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
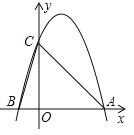
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图像上有一点D(x,y)(其中![]() ,
,![]() ),使
),使![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=2,AD=3,O为边AD上一点,以O为圆心,OA为半径r作⊙O,过点B作⊙O的切线BF,F为切点.
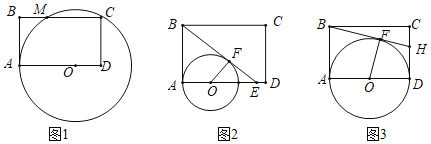
(1)如图1,当⊙O经过点C时,求⊙O截边BC所得弦MC的长度;
(2)如图2,切线BF与边AD相交于点E,当FE=FO时,求r的值;
(3)如图3,当⊙O与边CD相切时,切线BF与边CD相交于点H,设△BCH、四边形HFOD、四边形FOAB的面积分别为S1、S2、S3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015德阳)大华服装厂生产一件秋冬季外套需面料1.2米,里料0.8米,已知面料的单价比里料的单价的2倍还多10元,一件外套的布料成本为76元.
(1)求面料和里料的单价;
(2)该款外套9月份投放市场的批发价为150元/件,出现购销两旺态势,10月份进入批发淡季,厂方决定采取打折促销.已知生产一件外套需人工等固定费用14元,为确保每件外套的利润不低于30元.
①设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
②进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
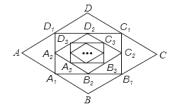
【题目】如图,在菱形![]() 中,边长为10,
中,边长为10,![]() .顺次连结菱形
.顺次连结菱形![]() 各边中点,可得四边形
各边中点,可得四边形![]() ;顺次连结四边形
;顺次连结四边形![]() 各边中点,可得四边形
各边中点,可得四边形![]() ;顺次连结四边形
;顺次连结四边形![]() 各边中点,可得四边形
各边中点,可得四边形![]() ;按此规律继续下去….则四边形
;按此规律继续下去….则四边形![]() 的周长是_________.
的周长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
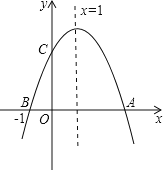
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为![]() ,则AK= .
,则AK= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com