
【题目】如图,![]() ,作
,作![]() 垂足为点
垂足为点![]() ,
,![]() 相交于点
相交于点![]() .
.
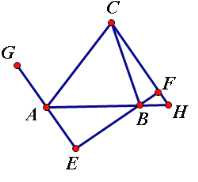
(1)求![]() 的度数.
的度数.
(2)求证:![]()
【答案】(1)∠E=90°;(2)见解析.
【解析】
(1)根据三角形外角的性质和角平分线的定义可得∠CAB+∠CBA=90°+![]() ∠E,然后在△ABC中利用三角形内角和定理可列式求出∠E;
∠E,然后在△ABC中利用三角形内角和定理可列式求出∠E;
(2)根据等角的余角相等可证∠BHC=∠BAE.
解:(1)∵∠GAB=∠E+∠ABE,∠ABF=∠E+∠BAE,
∴∠GAB+∠ABF=∠E+∠ABE+∠E+∠BAE=∠E+180°,
∵![]()
∴∠CAB=![]() ∠GAB,∠CBA=
∠GAB,∠CBA=![]() ∠ABF,
∠ABF,
∴∠CAB+∠CBA=![]() (∠GAB+∠ABF)=90°+
(∠GAB+∠ABF)=90°+![]() ∠E,
∠E,
∵∠CAB+∠CBA+∠ACB=180°,即90°+![]() ∠E+45°=180°,
∠E+45°=180°,
∴∠E=90°;
(2)∵CF⊥BF,
∴∠BFH=90°,
∴∠FBH+∠BHC=90°,
∵∠E=90°,
∴∠BAE+∠ABE=90°,
又∵∠ABE=∠FBH,
∴∠BHC=∠BAE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
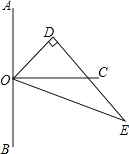
【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在线段AB上,(不与端点A、B重合),以点O为圆心,OA的长为半径画弧,线段BP与这条弧相切与点P,直线CD垂直平分PB,交PB于点C,交AB于点D,在射线DC上截取DE,使DE=DB。已知AB=6,设OA=r。
(1)求证:OP∥ED;
(2)当∠ABP=30°时,求扇形AOP的面积,并证明四边形PDBE是菱形;
(3)过点O作OF⊥DE于点F,如图所示,线段EF的长度是否随r的变化而变化?若不变,直接写出EF的值;若变化,直接写出EF与r的关系。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
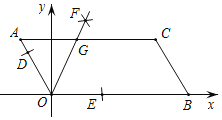
A. (![]() ﹣1,2) B. (
﹣1,2) B. (![]() ,2) C. (3﹣
,2) C. (3﹣![]() ,2) D. (
,2) D. (![]() ﹣2,2)
﹣2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.
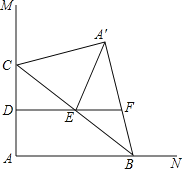
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生进行射击练习,两人在相同条件下各射击10次,将射击结果作统计分析如下:
命中环数 | 5 | 6 | 7 | 8 | 9 | 10 |
甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 |
乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
平均数 | 众数 | 方差 | |
甲 | 7 | 6 | 2.2 |
乙 |
(1)请你计算乙学生的相关数据并填入表中;
(2)根据你所学的统计学知识,利用上述某些数据评价甲、乙两人的射击水平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为_____m(结果保留整数,![]() ≈1.73).
≈1.73).
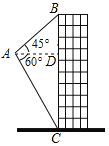
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() 两地相距240千米,乙车从
两地相距240千米,乙车从![]() 地驶向
地驶向![]() 地,行驶80千米后,甲车从
地,行驶80千米后,甲车从![]() 地出发驶向
地出发驶向![]() 地,甲车行驶5小时到达
地,甲车行驶5小时到达![]() 地,并原地休息.甲、乙两车匀速行驶,乙车速度是甲车速度的
地,并原地休息.甲、乙两车匀速行驶,乙车速度是甲车速度的![]() 倍.
倍.
(1)甲车的行驶速度是 千米/时,乙车的行驶速度是 千米/时;
(2)求甲车出发后几小时两车相遇;(列方程解答此问)
(3)若乙车到达![]() 地休息一段时间后按原路原速返回,且比甲车晚1小时到达
地休息一段时间后按原路原速返回,且比甲车晚1小时到达![]() 地.乙车从
地.乙车从![]() 地出发到返回
地出发到返回![]() 地过程中,乙车出发 小时,两车相距40千米.
地过程中,乙车出发 小时,两车相距40千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com