
【题目】如图,ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,求∠AEB的度数.
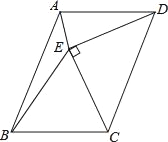
【答案】135°
【解析】
先证明AD=DE=CE=BC,得出∠DAE=∠AED,∠CBE=∠CEB,∠EDC=∠ECD=45°,设∠DAE=∠AED=x,∠CBE=∠CEB=y,求出∠ADC=225°-2x,∠BAD=2x-45°,由平行四边形的对角相等得出方程,求出x+y=135°,即可得出结果.
解:∵四边形ABCD是平行四边形,
∴AD=BC,∠BAD=∠BCD,∠BAD+∠ADC=180°,
∵AD=DE=CE,
∴AD=DE=CE=BC,
∴∠DAE=∠AED,∠CBE=∠CEB,
∵∠DEC=90°,
∴∠EDC=∠ECD=45°,
设∠DAE=∠AED=x,∠CBE=∠CEB=y,
∴∠ADE=180°﹣2x,∠BCE=180°﹣2y,
∴∠ADC=180°﹣2x+45°=225°﹣2x,∠BCD=225°﹣2y
,∴∠BAD=180°﹣(225°﹣2x)=2x﹣45°,
∴2x﹣45°=225°﹣2y,
∴x+y=135°,
∴∠AEB=360°﹣135°﹣90°=135°.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为8,点
的边长为8,点![]() 是边
是边![]() 上一动点(不与点
上一动点(不与点![]() 重合),以
重合),以![]() 为边在
为边在![]() 的下方作等边三角形
的下方作等边三角形![]() ,连接
,连接![]() .
.

(1)在运动的过程中,![]() 与
与![]() 有何数量关系?请说明理由.
有何数量关系?请说明理由.
(2)当BE=4时,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由;
(2)点P在滑动时,当AP长为多少时,△ADP与△BPC全等,为什么?
(3)点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只口袋里放着![]() 个红球、
个红球、![]() 个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.
个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.
![]() 取出红球的概率为
取出红球的概率为![]() ,白球有多少个?
,白球有多少个?
![]() 取出黑球的概率是多少?
取出黑球的概率是多少?
![]() 再在原来的袋中放进多少个红球,能使取出红球的概率达到
再在原来的袋中放进多少个红球,能使取出红球的概率达到![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】飞镖随机地掷在下面的靶子上.
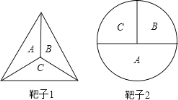
![]() 在每一个靶子中,飞镖投到区域
在每一个靶子中,飞镖投到区域![]() 、
、![]() 、
、![]() 的概率是多少?
的概率是多少?
![]() 在靶子
在靶子![]() 中,飞镖投在区域
中,飞镖投在区域![]() 或
或![]() 中的概率是多少?
中的概率是多少?
![]() 在靶子
在靶子![]() 中,飞镖没有投在区域
中,飞镖没有投在区域![]() 中的概率是多少?
中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=(2m+4)x,求:
(1)m为何值时,函数图象经过第一、三象限?
(2)m为何值时,y随x的增大而减小?
(3)m为何值时,点(1,3)在该函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若![]() ,试求线段CD的长度.
,试求线段CD的长度.

●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;

●推广应用
如图3,等腰△ABC为勾股高三角形,其中![]() ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若
,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若![]() ,试求线段DE的长度.
,试求线段DE的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com