
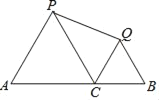
【题目】如图,AB=12,C是线段AB上一点,分别以AC、CB为边在A的同侧作等边△ACP和等边△CBQ,连接PQ,则PQ的最小值是( )
A. 3B. 4C. 5D. 6
【答案】D
【解析】
分别延长AP、BQ交于点D,易证四边形CPDQ为平行四边形,得出PD+DQ=PC+CQ=AC+BC=12,作△ABD的中位线MN,则MD=DN=MN=![]() AB,运用中位线的性质和等边三角形的性质求出MD=DN=MN=
AB,运用中位线的性质和等边三角形的性质求出MD=DN=MN=![]() AB,进而求得MD+DN=PD+DQ,得出PM=QN,作PE⊥MN,QF⊥MN,则PE∥QF,然后证得△PME≌△QNF,从而证得MN=EF,根据平行线间的距离得出PQ≥EF,从而求得PQ的最小值.
AB,进而求得MD+DN=PD+DQ,得出PM=QN,作PE⊥MN,QF⊥MN,则PE∥QF,然后证得△PME≌△QNF,从而证得MN=EF,根据平行线间的距离得出PQ≥EF,从而求得PQ的最小值.
解:如图,分别延长AP、BQ交于点D,
∵∠A=∠QCB=60°,
∴AD∥CQ,
∵∠B=CPCA=60°,
∴BD∥PC,
∴四边形CPDQ为平行四边形,
∴PD=CQ,PC=DQ,
∴PD+DQ=PC+CQ=AC+BC=12,
作△ABD的中位线MN,则MD=DN=MN=![]() AB,
AB,
∴MD+DN=AB=12,
∴MD+DN=PD+DQ,
∴PM=QN,
作PE⊥MN,QF⊥MN,
∴PE∥QF,
∴∠PEM=∠QFN=90°,且∠PME=∠QNF=60°,PM=QN
∴△PME≌△QNF(AAS),
∴EM=FN,
∴MN=EF,
∴PQ≥EF,
∴C是线段AB的中点时,PQ的值最小,最小值为![]() AB=6.
AB=6.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
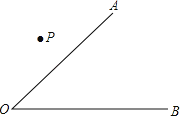
【题目】如图,已知∠AOB和点P.
(1)过点P画射线PM∥OA,PN∥OB,符合要求的图形有哪几种情况?请分别画出这些图形;
(2)在所画的图形中,∠MPN与∠AOB的大小有什么关系?
(3)你有什么发现?
查看答案和解析>>
科目:初中数学 来源: 题型:
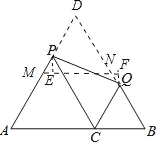
【题目】已知:如图,在平行四边形中,点E在BC边上,连接AE.O为AE中点,连接BO并延长交AD于F.
(1)求证:△AOF≌△BOE,
(2)判断当AE平分∠BAD时,四边形ABEF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形 AOBC 的三个顶点的坐标分别为 O(0,0),A(0,3), B(4,0),按以下步骤作图:①以点 O 为圆心,适当长度为半径作弧, 分别交 OC,OB 于点 D,E;②分别以点 D,E 为圆心,大于 ![]() DE 的长为半径作弧,两弧在∠BOC 内交于点 F;③作射线 OF,交边 BC于点 G,则点 G 的坐标为( )
DE 的长为半径作弧,两弧在∠BOC 内交于点 F;③作射线 OF,交边 BC于点 G,则点 G 的坐标为( )
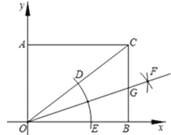
A. (4, ![]() )B. (
)B. ( ![]() ,4)C. (
,4)C. ( ![]() ,4)D. (4,
,4)D. (4, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
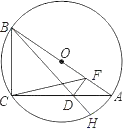
【题目】如图,△ABC是⊙O的内接三角形,直径AB=10.sinA=![]() ,点D为线段AC上一动点(不运动至端点A、C),作DF⊥AB于F,连结BD,井延长BD交⊙O于点H,连结CF.
,点D为线段AC上一动点(不运动至端点A、C),作DF⊥AB于F,连结BD,井延长BD交⊙O于点H,连结CF.
(1)当DF经过圆心O时,求AD的长;
(2)求证:△ACF∽△ABD;
(3)求CFDH的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
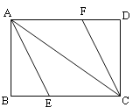
【题目】如图,在矩形ABCD中,AE平分∠BAC交BC于E,CF平分∠ACD交AD于F.
(1)试说明四边形AECF为平行四边形;
(2)探索:当矩形ABCD的边AB和BC满足什么数量关系时,四边形AECF为菱形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com