
【题目】已知:如图,在平行四边形中,点E在BC边上,连接AE.O为AE中点,连接BO并延长交AD于F.
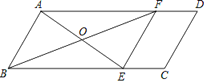
(1)求证:△AOF≌△BOE,
(2)判断当AE平分∠BAD时,四边形ABEF是什么特殊四边形,并证明你的结论.
【答案】(1)求证:见解析;(2)四边形ABEF是菱形,见解析.
【解析】
(1)先利用平行四边形的性质得AD∥BC,则∠AFB=∠CBF,然后根据“AAS”可判断△AOF≌△BOE;
(2)利用△AOF≌△BOE得到FO=BO,则可根据对角线互相平分可判定四边形ABEF是平行四边形,根据AE平分∠BAD,得∠BAE=∠FAE,又∠FAE=∠AEB,得∠BAE=∠AEB,AB=BE,有一组对边相等的平行四边形是菱形,得四边形ABEF是菱形.
(1)∵O为AE中点,
∴AO=EO,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFB=∠CBF,
在△AOF和△BOE中
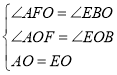 ,
,
∴△AOF≌△BOE;
(2)四边形ABEF是菱形,理由如下:
∵△AOF≌△BOE,
∴FO=BO,
而AO=EO,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠BAE=∠FAE,
∵∠FAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是菱形.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
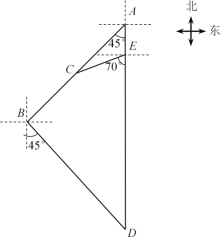
【题目】如图,港口B位于港口A的南偏西45°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的南偏东45°方向的D处,它沿正北方向航行18.5 km到达E处,此时测得灯塔C在E的南偏西70°方向上,求E处距离港口A有多远?
(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
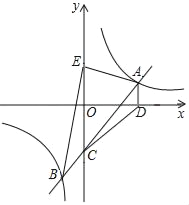
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.
(1)求一次函数和反比例函数的解析式;
(2)若点E是点C关于x轴的对称点,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,E为AB的中点,G为BC延长线上一点,射线EO与∠ACG的角平分线交于点F,若AB=8,BC=6,则线段EF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=12,C是线段AB上一点,分别以AC、CB为边在A的同侧作等边△ACP和等边△CBQ,连接PQ,则PQ的最小值是( )
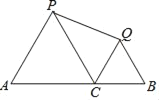
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )
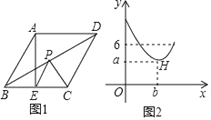
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
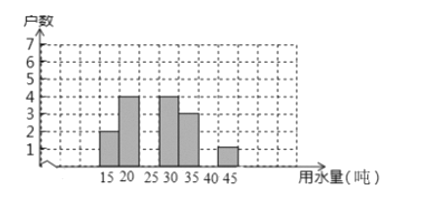
【题目】下表是2019年三月份某居民小区随机抽取20户居民的用水情况:
用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
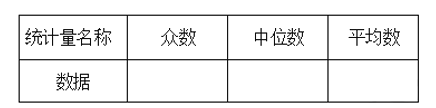
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
(3)为了倡导“节约用水,绿色环保”的意识,台州市自来水公司实行“梯级用水、分类计费”,价格表如下:

如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭在ⅠI级标准?并估算这些级用水户的总水费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
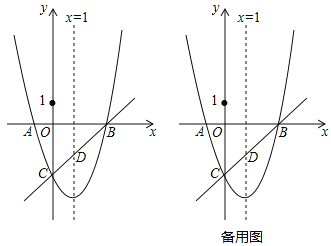
【题目】已知抛物线![]() 与x轴交于点A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
与x轴交于点A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求出抛物线的函数表达式;
(2)设点E时抛物线上一点,且S△ABE=![]() S△ABC,求tan∠ECO的值;
S△ABC,求tan∠ECO的值;
(3)点P在抛物线上,点Q在抛物线对称轴上,若以B、C、P、Q为顶点的四边形是平行四边形,求点P坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com