
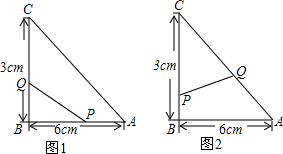
���� ��1���������t=2ʱ��BP��BQ��ֵ�����ݹ��ɶ������PQ�ij���
�ڸ���PQ��AC���õ�$\frac{BQ}{BC}$=$\frac{BP}{BA}$��������Ӧ�Ĵ���ʽ�������t��ֵ��
��2����QH��AB��BC��H����t��ʾ��CP��HQ�����������������ʽ�õ�һԪ���η��̣��ⷽ�̵õ��𰸣�
��� �⣺��1���ٵ�t=2��ʱ��AP=2����BP=4��BQ=4��
�ɹ��ɶ����ã�PQ=4$\sqrt{2}$cm��
��������ã�BP=6-t��BQ=2t��
��PQ��AC��
��$\frac{BQ}{BC}$=$\frac{BP}{BA}$����$\frac{2t}{3}$=$\frac{6-t}{6}$��
���t=$\frac{6}{5}$��
�൱t=$\frac{6}{5}$ʱ��PQ��AC��
��2��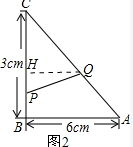 ��QH��AB��BC��H��
��QH��AB��BC��H��
��AB=6��BC=3��
��AC=3$\sqrt{5}$��
������ã�CQ=2t-3��CP=9-t��
��QH��AB��
��$\frac{CQ}{CA}$=$\frac{HQ}{AB}$����$\frac{2t-3}{3\sqrt{5}}$=$\frac{HQ}{6}$��
HQ=$\frac{4\sqrt{5}t-6\sqrt{5}}{5}$��
��$\frac{1}{2}$����9-t����$\frac{4\sqrt{5}t-6\sqrt{5}}{5}$=12.6��
���t=$\frac{21-\sqrt{333-\frac{252\sqrt{5}}{5}}}{4}$��
���� ���⿼����ǹ��ɶ�����Ӧ�á����������ε����ʺ�һԪ���η��̵�Ӧ�ã�����������������ε����ʡ���ȷ��������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
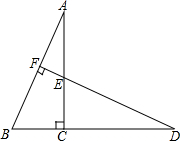 ��ͼ����ABC�У���ACB=90�㣬D��BC�ӳ�����һ�㣬DF��AB��F��DF��AC��E����һ�ң�ͼ���ж��ٸ�ֱ�������Σ����A��ȵĽ�����Щ�����A����Ľ�����Щ����ֱ�д������
��ͼ����ABC�У���ACB=90�㣬D��BC�ӳ�����һ�㣬DF��AB��F��DF��AC��E����һ�ң�ͼ���ж��ٸ�ֱ�������Σ����A��ȵĽ�����Щ�����A����Ľ�����Щ����ֱ�д�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | xy | B�� | y | C�� | x | D�� | x$\sqrt{y}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
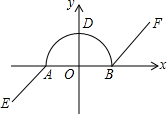 ��ͼ����ƽ��ֱ������ϵ�У����ǰ�����������AE��BF����ABΪֱ���İ�Բ����ɵ�ͼ�ν�����ͼ�Σ�ע�������߶�AB������֪A��-1��0����B��1��0����AE��BF���Ұ�Բ��y��Ľ���D������AE�ķ����ӳ����ϣ�
��ͼ����ƽ��ֱ������ϵ�У����ǰ�����������AE��BF����ABΪֱ���İ�Բ����ɵ�ͼ�ν�����ͼ�Σ�ע�������߶�AB������֪A��-1��0����B��1��0����AE��BF���Ұ�Բ��y��Ľ���D������AE�ķ����ӳ����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
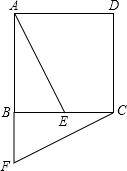 ��ͼ��������ABCD�У�EΪBC���ϵ�һ�㣬����ABE��ת��õ���CBF��
��ͼ��������ABCD�У�EΪBC���ϵ�һ�㣬����ABE��ת��õ���CBF���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com