
如图,抛物线y=ax2+bx﹣ 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,求⊙A的半径;
(3)在直线BC上方的抛物线上任取一点P,连接PB,PC,请问:△PBC的面积是否存在最大值?若存在,求出这个最大值的此时点P的坐标;若不存在,请说明理由.

解答: 解:(1)∵抛物线y=ax2+bx﹣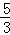 经过点A(1,0)和点B(5,0),
经过点A(1,0)和点B(5,0),
∴把A、B两点坐标代入可得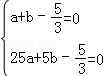 ,解得
,解得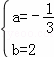 ,
,
∴抛物线解析式为y=﹣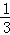 x2+2x﹣
x2+2x﹣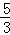 ;
;
(2)过A作AD⊥BC于点D,如图1,
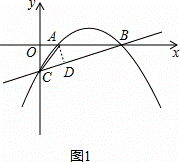
∵⊙A与BC相切,
∴AD为⊙A的半径,
由(1)可知C(0,﹣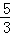 ),且A(1,0),B(5,0),
),且A(1,0),B(5,0),
∴OB=5,AB=OB﹣OA=4,OC=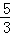 ,
,
在Rt△OBC中,由勾股定理可得BC=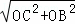 =
=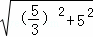 =
=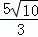 ,
,
∵∠ADB=∠BOC=90°,∠ABD=∠CBO,
∴△ABD∽△CBO,
∴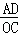 =
=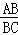 ,即
,即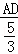 =
=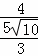 ,解得AD=
,解得AD=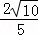 ,
,
即⊙A的半径为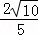 ;
;
(3)∵C(0,﹣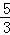 ),
),
∴可设直线BC解析式为y=kx﹣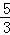 ,
,
把B点坐标代入可求得k=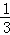 ,
,
∴直线BC的解析式为y=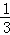 x﹣
x﹣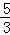 ,
,
过P作PQ∥y轴,交直线BC于点Q,交x轴于点E,如图2,
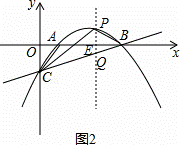
设P(x,﹣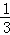 x2+2x﹣
x2+2x﹣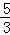 ),则Q(x,
),则Q(x,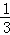 x﹣
x﹣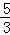 ),
),
∴PQ=(﹣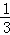 x2+2x﹣
x2+2x﹣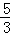 )﹣(
)﹣(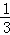 x﹣
x﹣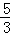 )=﹣
)=﹣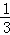 x2+
x2+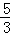 x=﹣
x=﹣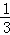 (x﹣
(x﹣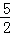 )2+
)2+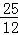 ,
,
∴S△PBC=S△PCQ+S△PBQ= PQ•OE+
PQ•OE+ PQ•BE=
PQ•BE= PQ(OE+BE)=
PQ(OE+BE)= PQ•OB=
PQ•OB=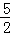 PQ=﹣
PQ=﹣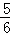 (x﹣
(x﹣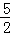 )2+
)2+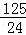 ,
,
∴当x=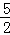 时,S△P
时,S△P BC有最大值
BC有最大值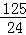 ,此时P点坐标为(
,此时P点坐标为(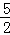 ,
, ),
),
∴当P点坐标为(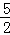 ,
, )时,△PBC的面积有最大值.
)时,△PBC的面积有最大值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=1,AB=2
(1)求作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)所作的圆中,求出劣弧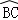 的长l.
的长l.

查看答案和解析>>
科目:初中数学 来源: 题型:
今年5月,某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:

(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com