
分析 设单开甲注油管需要x小时,则单开乙注油管需要(x-4)小时,由工程问题的数量关系建立方程求出其解即可.
解答 解:设单开甲注油管需要x小时,则单开乙注油管需要(x-4)小时,由题意得:
$(\frac{1}{x}+\frac{1}{x-4})×4+\frac{1}{x}×11=1$,
解得:x1=3,x2=20,
经检验,x1=3,x2=20都是原方程的根,但是x=3不符合实际,故舍去.
故甲单独开放注满油罐需要20小时,乙单独开放注满油罐需要16小时.
点评 本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,工程问题的数量关系的运用,解答时由工程问题的数量关系建立方程是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 有一组邻边相等的平行四边形是正方形 | |
| B. | 有一组邻边相等且有一角为直角的四边形为正方形 | |
| C. | 正方形是一组对边相等的矩形 | |
| D. | 正方形是有一个角为直角的菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
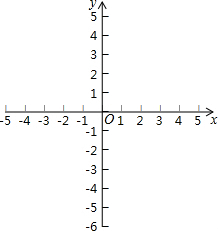 已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.
已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | B. | $\frac{\sqrt{7}-\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}-\sqrt{7}}{2}$ | D. | $\frac{-\sqrt{7}-\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
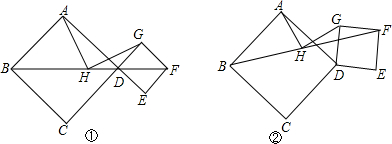
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com