
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��![]() ��C2��
��C2��![]() Ϊ���Ѻ������ߡ���
Ϊ���Ѻ������ߡ���
��1����������C2�Ľ���ʽ��
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
��3����������C2�Ķ���ΪC����B������Ϊ����1��4��������C2�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������C2�ϣ������������M�����꣬������˵�����ɣ�

���𰸡���1��![]() ����2��
����2��![]() ����3�����ڣ�M��1��2����1��5����
����3�����ڣ�M��1��2����1��5����
��������
�����������1�������y1�������꣬Ȼ���������������ߵĶ���������ͬ�����m��n��ֵ��
��2����A��a��![]() ������OQ=x��AQ=
������OQ=x��AQ=![]() ��Ȼ��õ�OQ+AQ��a�ĺ�����ϵʽ����������䷽�������OQ+AQ����ֵ��
��Ȼ��õ�OQ+AQ��a�ĺ�����ϵʽ����������䷽�������OQ+AQ����ֵ��
��3������BC������B����B��D��CM������ΪD��������֤����BCM�ա�MDB�䣬��ȫ�������ε����ʵõ�BC=MD��CM=B��D�����M������Ϊ��1��a�������ú�a��ʽ�ӿɱ�ʾ����B������꣬����B���������������ߵĽ���ʽ�����a��ֵ���Ӷ��õ���M�����꣮
����𡿽⣺��1����![]() =
=![]() ����������C1�Ķ�������Ϊ��1��4������������C1����C2������ͬ����
����������C1�Ķ�������Ϊ��1��4������������C1����C2������ͬ����![]() =1����1+m+n=4����ã�m=2��n=3����������C2�Ľ���ʽΪ
=1����1+m+n=4����ã�m=2��n=3����������C2�Ľ���ʽΪ![]() ��
��
��2����ͼ1��ʾ��
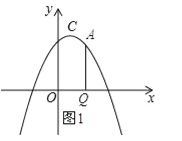
���A��������a��![]() ������AQ=
������AQ=![]() ��OQ=a����AQ+OQ=
��OQ=a����AQ+OQ=![]() =
=![]() =
=![]() ������a=
������a=![]() ʱ��AQ+OQ�����ֵ�����ֵΪ
ʱ��AQ+OQ�����ֵ�����ֵΪ![]() ��
��
��3����ͼ2��ʾ������BC������B����B��D��CM������ΪD��

��B����1��4����C��1��4���������ߵĶԳ���Ϊx=1����BC��CM��BC=2���ߡ�BMB��=90�㣬���BMC+��B��MD=90�㣮��B��D��MC�����MB��D+��B��MD=90�㣬����MB��D=��BMC���ڡ�BCM�͡�MDB���У��ߡ�MB��D=��BMC����BCM=��MDB����BM=MB�������BCM�ա�MDB�䣬��BC=MD��CM=B��D�����M������Ϊ��1��a������B��D=CM=4��a��MD=CB=2������B�������Ϊ��a��3��a��2������![]() �������ã�
�������ã�![]() �����a=2����a=5��
�����a=2����a=5��
��a=2ʱ��M������Ϊ��1��2������a=5ʱ��M������Ϊ��1��5����
������������M������Ϊ��1��2����1��5��ʱ��B��ǡ������������C2�ϣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����5��3x2y��xy2����4����xy2+3x2y����ֵ������|x+2|+��y��3��2��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��֪ʶ��������20���⣬ÿһ���Ե�10�֣������5��.С���÷�Ҫ����90�֣�������Ҫ��Զ��ٵ��⣿����С�������x���⣬����������г��IJ���ʽΪ( )
A.10x+5(20��x)��90B.10x+5(20��x)��90
C.10x��5(20��x)��90D.10x��5(20��x)��90
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A. a2+a3=a5 B. (a2)3=a5 C. (a+b)2=a2+b2 D. a6��a2=a4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε����߳��ֱ�Ϊ6�M��3�M����õ��������ε��ܳ����� ��
A. 9�M B. 12�M C. 12�M��15�M D. 15�M
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����0.22��105�ijɿ�ѧ����������ʽ����ȷ���ǣ�������
A.2.2��103
B.2.2��104
C.2.2��105
D.2.2��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015�ꡰʥ�س������������ݸ�װ�����ܲ�ֵΪ14.966��Ԫ������14.966��Ԫ�ÿ�ѧ��������ʾΪԪ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com