
分析 (1)易证点P、M和两个切点组成的四边形是正方形,从而PM=2,设P坐标为(t,t2),则t2+(t2-2)2=22,求出t的值即可,进而得到点P的坐标;
(2)分两种情况进行讨论,①若直线l平行与y轴,②若直线l不平行与y轴,设直线l的解析式为y=kx+b,根据直线l与抛物线y=x2只有一个公共点求出k的值,进而根据点到直线的距离公式求出点M与直线的距离.
解答 解:(1)设两个切点分别为A、B,
如图所示: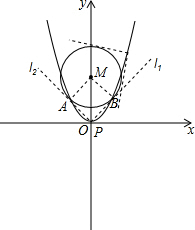
∵MA⊥AP,MB⊥PB,且l1⊥l2,
∴四边形APBM是正方形,
∵AM=$\sqrt{2}$,
∴PM=$\sqrt{A{M}^{2}+A{P}^{2}}$=2,
设设P坐标为(t,t2),则t2+(t2-2)2=22,
解得t=0或t=$±\sqrt{3}$,
∴点P的坐标为(0,0)、($\sqrt{3},3$)、($-\sqrt{3},3$);
(2)①若直线l平行与y轴,直线l即x=2,此时点M与直线l的距离为2;
②若直线l不平行与y轴,
设直线l的解析式为y=kx+b,
∵直线l过(2,4)点,
∴4=2k+b,
∴b=4-2k,
∴直线l解析式为y=kx+4-2k,
∵直线l与抛物线y=x2只有一个公共点,
∴kx+4-2k=x2只有一个根,
∴k2-8k+16=0,
∴k=4,
∴直线l解析式为y=4x-4,
∴点M(0,2)与直线l的距离d=$\frac{|-2-4|}{\sqrt{{1}^{2}+{4}^{2}}}$=$\frac{{6\sqrt{17}}}{17}$.
点评 本题主要考查了二次函数的综合题的知识,解答本题的关键是求出PM的长为2,解答(2)问时注意垂直于x轴的直线不能漏解,此题难度一般.


科目:初中数学 来源: 题型:解答题
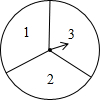 2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.
2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
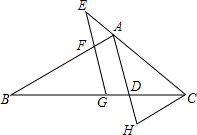 如图,在△ABC中,G为BC的中点,E为CA延长线上一点,EG交AB于F,AD∥EG交BC于点D,CH∥AB交AD延长线于点H,且EC=k•AC,探究:FB与CH的数量关系.
如图,在△ABC中,G为BC的中点,E为CA延长线上一点,EG交AB于F,AD∥EG交BC于点D,CH∥AB交AD延长线于点H,且EC=k•AC,探究:FB与CH的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
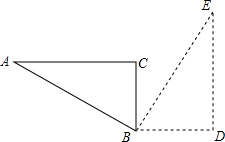 如图,Rt△ABC中,∠A=30°,AB=4cm,将△ABC绕顶点B按顺时针方向旋转90°到△BDE的位置,则:
如图,Rt△ABC中,∠A=30°,AB=4cm,将△ABC绕顶点B按顺时针方向旋转90°到△BDE的位置,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
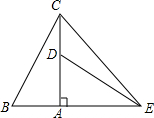 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC绕点A顺时针旋转90°得到(点D与点B是对应点,点E与点C是对应点),连接CE,则∠CED的度数是( )
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC绕点A顺时针旋转90°得到(点D与点B是对应点,点E与点C是对应点),连接CE,则∠CED的度数是( )| A. | 45° | B. | 30° | C. | 25° | D. | 15° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com