
����Ŀ����ͼ������ABC�У���C��90����AB��10cm��BC��8cm����P�ӵ�A��ʼ������AC���C��2cm/s���ٶ��ƶ������ͬʱ����Q�ӵ�C��ʼ�ر�CB���B��1cm/s���ٶ��ƶ������P��Q�ֱ��A��Cͬʱ�������˶���ʱ��Ϊts������Q�˶�����Bʱ������ֹͣ�˶���

��1������P���߶�AC���˶�ʱ��P��C����֮��ľ����� ��cm�����ú�t�Ĵ���ʽ��ʾ��
��2�����˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ����PQC���������ABC�����![]() �������ڣ���t��ֵ���������ڣ�˵�����ɣ�
�������ڣ���t��ֵ���������ڣ�˵�����ɣ�
���𰸡���1����6��2t������2�����ڣ����ɼ�������t��4
��������
��1������AC��6cm��AP��2t�����ɵõ�������P���߶�AC���˶�ʱ��P��C����֮��ľ��루6��2t��cm��
��2���������������0��t��3ʱ����3��t��8ʱ���ֱ�������PQC���������ABC�����![]() ���з�����⼴�ɣ�
���з�����⼴�ɣ�
�⣺��1���ߡ�ABC�У���C��90����AB��10cm��BC��8cm��
���ɹ��ɶ�����AC��6cm��
�֡ߵ�P�ӵ�A��ʼ������AC���C��2cm/s���ٶ��ƶ���
��AP��2t��
�൱��P���߶�AC���˶�ʱ��P��C����֮��ľ��루6��2t��cm��
�ʴ�Ϊ����6��2t����
��2����ABC�����ΪS��ABC��![]() ��6��8��24��
��6��8��24��
�ٵ�0��t��3ʱ��PC��6��2t��QC��t��
��S��PCQ��![]() PC��QC��
PC��QC��![]() t��6��2t����
t��6��2t����
��![]() t��6��2t����4��
t��6��2t����4��
��t2��3t+4��0��
�ߡ���b2��4ac����7��0��
���һԪ���η�����ʵ������
��÷�Χ�²����ڣ�
�ڵ�3��t��8ʱ��PC��2t��6��QC��t��
��S��PCQ��![]() PC��QC��
PC��QC��![]() t��2t��6����
t��2t��6����
��![]() t��2t��6����4��
t��2t��6����4��
��t2��3t��4��0��
���t��4��1����ȥ����
�������������ڣ���t��4ʱ����PQC���������ABC�����![]() ��
��


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ�����װ�к졢��������ɫ��С����Щ�����ɫ�ⶼ��ͬ�����к�����1�����������������һ����������ǰ���ĸ���Ϊ![]() ��
��
��1��������а���ĸ���������ͨ����ʽ���з��̽��
��2���������һ����Żز����ȣ����������һ���������ζ�������ͬ��ɫ��С��ĸ��ʣ���������״ͼ���б����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ʒ�̳�Ԥ��ijƷ���˶����ܹ�����������32000Ԫ������һ�������˶��������к�ܿ��������̳�����68000Ԫ�����ڶ��������˶��������������ǵ�һ������������2������ÿ���۶���10Ԫ��
��1�����̳����ι����������˶��������ף�
��2������������˶���ÿ���ۼ���ͬ����ȫ���������������20%����ôÿ���ۼ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y��ax2��4ax��![]() ��a��0����x����A��B���㣬��y���ڵ�C�����������ߵĶ���ΪD��
��a��0����x����A��B���㣬��y���ڵ�C�����������ߵĶ���ΪD��
��1�����D�����꣮
��2������C��CE��x�ύ�������ڵ�E����CE��2ABʱ�����D�����꣮
��3��������������ֱ��y����x�ཻ������һ������ĺ�����Ϊ��1������P��m��0����x��Ĵ��ߣ��������������ڵ�M����ֱ��y����x�ڵ�N���ҵ�M�ڵ�N���·������߶�MN�ij�����m�����������ʱ����m��ȡֵ��Χ��
��4����Q���������������˶�������������������ֻ����������Q������S��ABQ��3S��ABC��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB��90����AC��4��BC��3��P��AC�ϵ�һ�㣬PH��AB�ڵ�H����PHΪֱ������O����CH��PB�Ľ������ڡ�O��ʱ��AP��ֵΪ��������
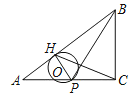
A.![]() B.
B.![]() C.2D.3
C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ŵ�С����״����ͬ�Ŀ�Ƭ�Ϸֱ�д������1��2��3��4�������Ƿ��벻���ĺ�����ҡ�ȣ�
��1������������1�ſ�Ƭ������Ŀ�Ƭ�ϵ�����ǡ����ż���ĸ���Ϊ�� ����
��2������������1�ſ�Ƭ����¼���ֺ�Ż�ҡ�ȣ��ٳ��һ�ſ�Ƭ����¼���֣�����״ͼ���б��������γ���Ŀ�Ƭ�ϵ�����ǡ�����������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߶�AB�Ķ˵�����ֱ�ΪA��0��6����B��6��6������Q���߶�AB�ϣ���QΪ����������y����![]() x2+bx+c��y�ύ�ڵ�D����x���һ������ΪC�����Q�ĺ�����Ϊm����C�ĺ�����Ϊn��n��m����
x2+bx+c��y�ύ�ڵ�D����x���һ������ΪC�����Q�ĺ�����Ϊm����C�ĺ�����Ϊn��n��m����
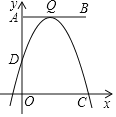
��1����m��0ʱ����n��ֵ��
��2�����߶�AD�ij����ú�m��ʽ�ӱ�ʾ����
��3����P��2��0����x���ϣ�����BPD�����ΪS����S��m�Ĺ�ϵʽ��
��4������DCQ����QCΪֱ�DZߵ�ֱ��������ʱ��ֱ��д��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳���6����A��60�㣬E��AD���е㣬F��AB����һ�����㣬EG��EF�ҡ�GEF��60�㣬��GB+GC����Сֵ��_____
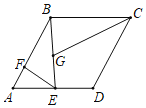
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��30Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����70Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 40 | 50 | 60 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ������W��x֮��ĺ�������ʽ������=�����ɱ�����
��3����˵����2����������W���ۼ�x�ı仯���仯���������ָ���ۼ�Ϊ����Ԫʱ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com