
����Ŀ������֪����̸������һ���ľ�����������������һ�㣬�ɼ����ӣ��Ӳ��ֵ����壬�ɵ�ά����ά��֪ʶ�뷽���ϵ������̽����չ����Ҫ;������˼�뷧�ŷ��������⡢�½��۵���Ҫ������
���磬��֪ab��1����![]() ��ֵ��
��ֵ��
�⣺��ab��1����a2b2��1����ԭʽ![]()
�������ڡ��������⡷��ָ�����������ҵ���һ���ٹ���������һ�����ֺ����Ĵ��������������dz�Ⱥ��������
��������Ϸ��������֪ab��1�����![]() �Ľ����_____��
�Ľ����_____��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��ijѧϰС����̽��������ȫ��ʱ���������������ֵ��͵Ļ���ͼ�Σ���ͼ�٣���֪���ڡ�ABC�У���BAC=90�㣬AB=AC��ֱ��L������A��BD��ֱ��L��CE��ֱ��L������ֱ�Ϊ��D��E��֤����DE=BD+CE��
��2����ԱС���룬��������Dz���ֱ�ǣ��ǽ����Ƿ������أ���ͼ�ڣ�����1���е�������Ϊ���ڡ�ABC�У�AB=AC��D��A��E���㶼��ֱ��L�ϣ������С�BDA=��AEC=��BAC=����������Ϊ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ��������������������֤����������������˵�����ɣ�
��3����ѧ��ʦ���������ǵ�̽���������������������֪ʶ��������⣺��ͼ�ۣ�����ABC�ı�AB��AC������������ABDE��������ACFG��AH��BC���ϵĸߣ��ӳ�HA��EG�ڵ�I����֤��I��EG���е㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳�����ۺ���ʵ�����ϣ�ͬѧ��������֪���������ߵij��ȣ��������������Ϊ���չ��ѧ���Сӱ�뵽�������������������⡣ͼ1��ͼ2����8��8������������ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ����Ϊ��㡣
�������֣�Сӱ��ͼ1�л�����ABC���䶥��A��B��C���Ǹ�㣬ͬʱ����������BDEF��ʹ���Ķ��㶼�ڸ���ϣ������ı�DE��EF�ֱ���C��A����������ͼ����ˡ�ABC�������
��1����ͼ1�У�Сӱ�����ġ�ABC�����߳��ֱ���AB= ��BC= ��AC= ����ABC�����Ϊ ��
��2���������Сӱ��˼·����ͼ2���Ը��Ϊ���㻭һ����DEF��ʹ���������߳��ֱ�Ϊ2��![]() ��
��![]() ����ֱ��д����DEF�����= ��
����ֱ��д����DEF�����= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ������ֱ�������ΰ�ͼʾ��ʽ���η��ۣ���DE=a��������˵����ȷ������____��
��DC��ƽ�֡�BDE����BC��Ϊ![]() ���ۡ�
���ۡ�![]() �ǵ��������Σ��ܡ�CED���ܳ�����BC�ij���
�ǵ��������Σ��ܡ�CED���ܳ�����BC�ij���

A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD//BC����A=90����EΪAB��һ�㣬��AE=BC����1=��2.
��˵������1����ADE����BECȫ������˵�����ɣ�
��2���ж���CDE����״����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
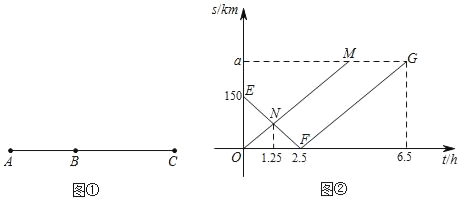
����Ŀ����ͼ�٣�A��B��C����������һֱ���ϣ����������ס��ҷֱ��A��B����ͬʱ����ʻ��C�أ���ͼ�ڣ�������������ʻ�����е�C�صľ���s��km������ʻʱ��t��h���Ĺ�ϵͼ���������߶�EF��FG�Ǽ׳���ͼ���߶�OM���ҳ���ͼ��
��1��ͼ���У�a��ֵΪ�� ������M������Ϊ�� ����
��2�����׳����ҳ���B�ص��е�λ��ʱ������ʻ��ʱ��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
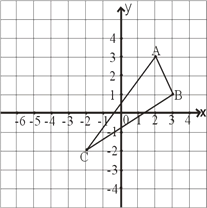
����Ŀ����ͼ����֪��ABC����������ֱ�ΪA��2��3����B��3��1����C����2����2��.
��1������ͼ��������ABC����y��Գ�ͼ����DEF��A��B��C�Ķ�Ӧ��ֱ���D��E��F������ֱд��D��E��F������.D��E��F��������ǣ�D( , ) E( , ) F( , )��
��2�����ı���ABED�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼȡ�����ҹ��Ŵ���ѧ����ˬ�ġ�����Բ��ͼ�������ĸ�ȫ�ȵ�ֱ�����������м��С������ƴ�ɵ�һ��������������������ε������13��С�����ε������4��ֱ�������εĽ϶�ֱ�DZ�Ϊa���ϳ�ֱ�DZ�Ϊb����ô![]() ��ֵΪ______________.
��ֵΪ______________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1����x���һ������A�ڵ㣨��3��0���ͣ���2��0��֮�䣬�䲿��ͼ����ͼ�������н��ۣ���4ac��b2��0����2a��b=0����a+b+c��0������M��x1��y1����N��x2��y2�����������ϣ���x1��x2����y1��y2��������ȷ���۵ĸ����ǣ� ��
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com