
【题目】小民对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为
的值为![]() 时,函数值为
时,函数值为![]() ;当自变量的值为
;当自变量的值为![]() 时,函数值为
时,函数值为![]() .探究过程如下,请补充完整,
.探究过程如下,请补充完整,
(1)求这个函数的表达式;
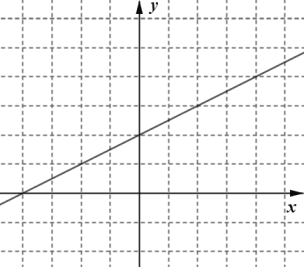
(2)在给出的平面直角坐标系中画出这个函数的图象并写出这个函数的一条性质:___________;
(3)进一步探究函数图象并解决问题:已知函数![]() 的图象如图所示,请结合你所画的函数图象,直接写出不等式
的图象如图所示,请结合你所画的函数图象,直接写出不等式![]() 的解集:___________.
的解集:___________.
【答案】(1)y1=|x-2|+![]() |x|;(2)当x=2时,此函数有最小值1;(3)x≥4或x≤0.
|x|;(2)当x=2时,此函数有最小值1;(3)x≥4或x≤0.
【解析】
(1)把(1,![]() ),(-1,
),(-1,![]() )代入
)代入![]() 可得关于a、b的二元一次方程组,解方程组求出a、b的值即可得答案;
可得关于a、b的二元一次方程组,解方程组求出a、b的值即可得答案;
(2)分x<0,0≤x<2,x≥2三种情况,分别利用描点法画出图象,根据图象写出相关性质即可;
(3)根据图象找出![]() 的图象在
的图象在![]() 图象上方的部分所对应的x的取值范围即可.
图象上方的部分所对应的x的取值范围即可.
(1)∵当自变量![]() 的值为
的值为![]() 时,函数值为
时,函数值为![]() ;当自变量的值为
;当自变量的值为![]() 时,函数值为
时,函数值为![]() ,
,
∴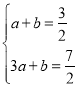 ,
,
解得:![]() ,
,
∴这个函数的表达式为y1=|x-2|+![]() |x|.
|x|.
(2)列表如下:
x | …… | -2 | -1 | 0 | 1 | 2 | 3 | 4 | …… |
y1 | …… | 5 |
| 2 |
| 1 |
| 4 | …… |
当x<0时,y1=![]() x+2,
x+2,
当0≤x<2时,y1=![]() x+2,
x+2,
当x≥2时,y1=![]() x-2,
x-2,
∴描点画图如下:
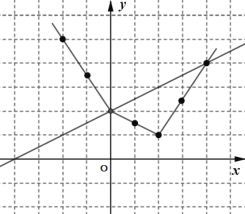
由图象可知:当x=2时,此函数有最小值1.
(3)由图象可知:x≥4或x≤0时,![]() 的图象在
的图象在![]() 图象上方,
图象上方,
∴不等式![]() 的解集为:x≥4或x≤0.
的解集为:x≥4或x≤0.
故答案为:x≥4或x≤0


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
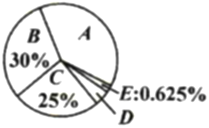
【题目】十九大召开后,某社区开展了“市民对十九大的关注情况”调查,采用随机抽样的方法访问了部分年龄在18周岁以上的城乡居民.小聪根据调查数据绘制了如下不完整的频数分布置表和扇形统计图.请根据图表解答下列问题.
关注情况 | 频数 |
非常关注( | 128 |
比较关注( | |
一般关注( | 80 |
不太关注( | |
不关注( | 2 |
(1)请完成频数分布表空格数据填写;
(2)求“非常关注”部分扇形圆心角的度数;
(3)若该社区18周岁以上居民共有20000人,请估计“比较关注”和“非常关注”的居民共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长均为1,
的正方形网格中,每个小正方形的边长均为1,![]() 的三个顶点均在小正方形的顶点上.
的三个顶点均在小正方形的顶点上.
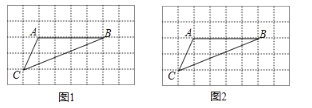
(1)在图1中画一个![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是轴对称图形;
为顶点的四边形是轴对称图形;
(2)在图2中画![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是中心对称图形;
为顶点的四边形是中心对称图形;
(3)直接写出图2中四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小猪佩奇随机坐到![]() 座位的概率是________;
座位的概率是________;
(2)若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形具有不稳定性,如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 在
在![]() 轴上,且点
轴上,且点![]() ,边
,边![]() 长为
长为![]() .现固定边
.现固定边![]() ,向右推动矩形使点
,向右推动矩形使点![]() 落在
落在![]() 轴上(落点记为
轴上(落点记为![]() ),点
),点![]() 的对应点记为
的对应点记为![]() ,已知矩形
,已知矩形![]() 与推动后形成的平行四边形
与推动后形成的平行四边形![]() 的面积比为
的面积比为![]() ,则点
,则点![]() 坐标为_______.
坐标为_______.
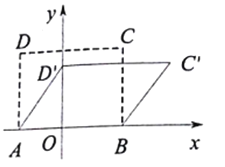
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的直径
的直径![]() ,点
,点![]() 是
是![]() 延长线上的一点,过
延长线上的一点,过![]() 点作
点作![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() .
.

(1)若![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,你认为
,你认为![]() 的大小是否发生变化?若变化,请说明理由;若不变化,求出
的大小是否发生变化?若变化,请说明理由;若不变化,求出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 为射线
为射线![]() 上一定点,点
上一定点,点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,满足
,满足![]() 为钝角,以点
为钝角,以点![]() 为中心,将线段
为中心,将线段![]() 逆时针旋转
逆时针旋转![]() 至线段
至线段![]() ,满足点
,满足点![]() 在射线
在射线![]() 的反向延长线上.
的反向延长线上.
(1)依题意补全图形;
(2)当点![]() 在运动过程中,旋转角
在运动过程中,旋转角![]() 是否发生变化?若不变化,请求出
是否发生变化?若不变化,请求出![]() 的值,若变化,请说明理由;
的值,若变化,请说明理由;
(3)从点![]() 向射线
向射线![]() 作垂线,与射线
作垂线,与射线![]() 的反向延长线交于点
的反向延长线交于点![]() ,探究线段
,探究线段![]() 和
和![]() 的数量关系并证明.
的数量关系并证明.
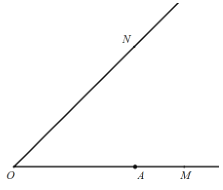
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工厂同时加工一批机器零件.甲工厂先加工了两天后停止加工,维修设备,当维修完设备时,甲乙两厂加工的零件数相等,甲工厂再以原来的工作效率继续加工这批零件.甲乙两厂加工零件的数量![]() (件),
(件),![]() (件)与加工件的时间
(件)与加工件的时间![]() (天)的函数图象如图所示,
(天)的函数图象如图所示,

(1)乙工厂每天加工零件的数为_____件;
(2)甲工厂维修设备的时间是多少天?
(3)求甲维修设备后加工零件的数量![]() (件)与加工零件的时间
(件)与加工零件的时间![]() (天)的函数关系式,并写出自变量
(天)的函数关系式,并写出自变量![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com