
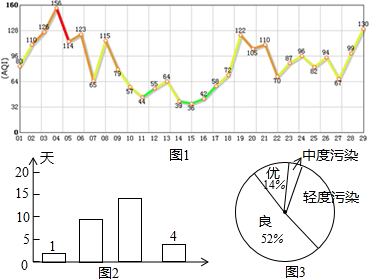
���� ��1������ͼ1�е������������ĸ��ȼ�����Ŀ����ȫͼ2����ͼ2���жȡ������Ⱦ�����ֱ�����������ðٷ��ʣ���ȫͼ3��
��2�������Ⱦ������Բ�ĽǵĶ���=�����Ⱦ�ٷ��ʡ�360�㣻
��3��һ��Ŀ�������Ϊ����������=365����������ռ����������ñ�����
��� �⣺��1����ȫͳ��ͼ���£�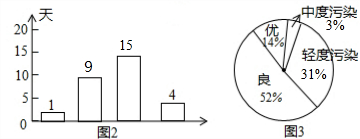
��2�������Ⱦ������Բ�ĽǵĶ���Ϊ��31%��360���112�㣻
��3��2016��һ�꺼�ݵĿ�������Ϊ����������Ϊ��$\frac{15+4}{29}$��365��239���죩��
���� ������Ҫ����������ͳ��ͼ������ͳ��ͼ������ͳ��ͼ���Ӳ�ͬ��ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼ������ر�ʾ��ÿ����Ŀ�����ݣ�����ͳ��ͼֱ�ӷ�ӳ����ռ����İٷֱȴ�С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
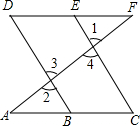 ��ͼ��E��ΪDF�ϵĵ㣬BΪAC�ϵĵ㣬��1=��2����C=��D����֤��
��ͼ��E��ΪDF�ϵĵ㣬BΪAC�ϵĵ㣬��1=��2����C=��D����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
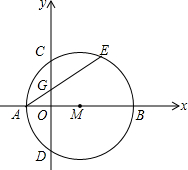 ��ͼ����ƽ��ֱ������ϵxOy�У���M��x����������ϣ���M��x����A��B���㣬��y����C��D���㣬��CΪ��AE���е㣬AE��y����G�㣬����A������Ϊ��-1��0����AE=4��
��ͼ����ƽ��ֱ������ϵxOy�У���M��x����������ϣ���M��x����A��B���㣬��y����C��D���㣬��CΪ��AE���е㣬AE��y����G�㣬����A������Ϊ��-1��0����AE=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
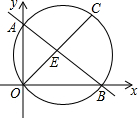 ��ͼ��ֱ��y=-$\frac{3}{4}$x+6��x���ڵ�B����y���ڵ�A����ABΪֱ����Բ����C��$\widehat{AB}$���е㣬����OC��ֱ��AB�ڵ�E����OC�ij�Ϊ7$\sqrt{2}$��
��ͼ��ֱ��y=-$\frac{3}{4}$x+6��x���ڵ�B����y���ڵ�A����ABΪֱ����Բ����C��$\widehat{AB}$���е㣬����OC��ֱ��AB�ڵ�E����OC�ij�Ϊ7$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com