练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
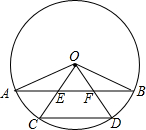
    AB、CD是⊙O的弦，OC、OD分别交AB于点E、F，且OE=OF．求证：
    AC
    =
    BD
    ．
    考点：圆心角、弧、弦的关系
    专题：证明题
    分析：过点O作OG⊥AB于点G，延长OG与⊙O交于H．先由等腰三角形三线合一的性质得出∠EOG=∠FOG，利用圆心角、弧、弦间的关系可以推知
    CH
    =
    DH
    ；然后根据垂径定理可知
    AH
    =
    BH
    ；最后根据图形易证得结论．
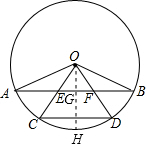    解答：证明：过点O作OG⊥AB于点G，延长OG与⊙O交于H．
    ∵OE=OF，OG⊥EF于点G，
    ∴∠EOG=∠FOG，
    ∴
    CH
    =
    DH
    ．
    又∵OG⊥AB于点G，
    ∴
    AH
    =
    BH
    ，
    ∴
    AH
    -
    CH
    =
    BH
    -
    DH
    ，
    即
    AC
    =
    BD
    ．
    点评：本题考查了垂径定理，圆心角、弧、弦的关系，等腰三角形的性质．解答本题时，通过作辅助线OH构建等弧（
    CH
    =
    DH
    ；
    AH
    =
    BH
    ）来证明结论．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，点D、E、F分别在等边△ABC的三边AB、BC、CA上，且△DEF也是等边三角形，求证：AD=BE=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    抛物线y=2+6x-x2的顶点坐标为（　　）
    A、（3，11）
    B、（-3，-25）
    C、（
    3
    2
    ，
    35
    4
    ）
    D、（6，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    画一个封闭的凸四边形，同旁内角有
     
    对；画一个凸五边形，同旁内角有
     
    对；探究凸n边形中，同旁内角有
     
    对．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，点O是直线AD上一点，射线OC、OE分别是∠AOB、∠BOD的平分线，∠COE=（　　）°．
    A、60B、70
    C、90D、不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    己知：如图，点E、C在线段BF上，BE=CF，AB∥DE，AC∥DF．求证：△ABC≌△DEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    当x=1时，代数式px3+qx-1的值是2014，则当x=-1时，代数式px3+qx-1的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

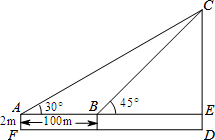    如图，为了测量建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了100m，此时自B处测得建筑物顶部的仰角是45°．已知测角仪的高度是2m，请你计算出该建筑物的高度．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

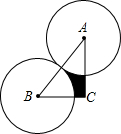    如图在直角△ABC中，∠ACB=90°，AC=8cm，BC=6cm，分别以A、B为圆心，以
    AB
    2
    的长为半径作圆，将直角△ABC截去两个扇形，则剩余（阴影）部分的面积为（　　）
    A、(24-
    25
    4
    π)cm2
    B、
    25
    4
    πcm2
    C、(24-
    5
    8
    π)cm2
    D、(24-
    25
    6
    π)cm2

    查看答案和解析>>

    同步练习册答案